
【题目】求满足如下条件的最小正整数![]() :在
:在![]() 的圆周上任取
的圆周上任取![]() 个点
个点![]() ,则在
,则在![]() 个
个![]() 中,至少有2007个不超过
中,至少有2007个不超过![]() .
.
【答案】91
【解析】
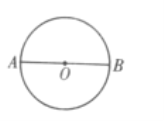
首先,当![]() 时,如图,设
时,如图,设![]() 是
是![]() 的直径,在点
的直径,在点![]() 和
和![]() 的附近分别取45个点,此时,只有
的附近分别取45个点,此时,只有![]() 个角不超过
个角不超过![]() .所以,
.所以,![]() 不满足题意.
不满足题意.
其次,当![]() 时,接下来证明:至少有2007个角不超过
时,接下来证明:至少有2007个角不超过![]() .
.
对圆周上的91个点![]() ,若
,若![]() ,则联结
,则联结![]() ,这样就得到一个图
,这样就得到一个图![]() .设图
.设图![]() 中有
中有![]() 条边.
条边.
当![]() ,
,![]() 时,
时,![]() ,故图
,故图![]() 中没有三角形.
中没有三角形.
若![]() ,则有
,则有![]() 个角不超过
个角不超过![]() ,命题得证.
,命题得证.
若![]() ,不妨设
,不妨设![]() 、
、![]() 之间有边相连,因为图中没有三角形,所以,对于点
之间有边相连,因为图中没有三角形,所以,对于点![]() ,它至多与
,它至多与![]() 、
、![]() 中的一个有边相连.从而,
中的一个有边相连.从而,![]() ,其中,
,其中,![]() 表示从
表示从![]() 处引出的边数.又
处引出的边数.又![]() ,而对图
,而对图![]() 中每一条边的两个顶点
中每一条边的两个顶点![]() 、
、![]() ,都有
,都有![]() .
.
于是,上式对每一条边求和可得![]() .
.
由柯西不等式得
![]()
![]() .
.
故![]()
![]() ,
,![]() .
.
因此,91个顶点中,至少有![]() 个点对,它们之间没有边相连.从而,对应的顶点所对应的角不超过
个点对,它们之间没有边相连.从而,对应的顶点所对应的角不超过![]() .
.
综上所述,![]() 的最小值为91.
的最小值为91.


科目:高中数学 来源: 题型:
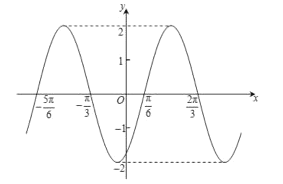
【题目】函数![]() 的图象如图所示,为了得到函数
的图象如图所示,为了得到函数![]() 的图象,可以把函数
的图象,可以把函数![]() 的图象( )
的图象( )
A.先向左平移![]() 个单位,再把所得各点的横坐标伸长到原来的
个单位,再把所得各点的横坐标伸长到原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
B.先向左平移![]() 个单位,再把所得各点的横坐标缩短到原来的
个单位,再把所得各点的横坐标缩短到原来的![]() (纵坐标不变)
(纵坐标不变)
C.每个点的横坐标缩短到原来的![]() (纵坐标不变),再向左平移
(纵坐标不变),再向左平移![]() 个单位
个单位
D.每个点的横坐标伸长到原来的![]() 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面a内作菱形ABCD,边长为1,∠BAD=60°,再在a的上方,分别以△ABD与△CBD为底面安装上相同的正棱锥P-ABD与Q-CBD,∠APB=90°.

(1)求二面角P-BD-Q的余弦值;
(2)求点P到平面QBD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com