
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() 过点
过点![]() ,且椭圆
,且椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且不垂直于
且不垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:直线
,证明:直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
试题分析:(1)根据题中条件运用基本量之间的关系求解;(2)借助题设条件运用直线和椭圆的位置关系建立坐标之间的关系,再用坐标之间的关系分析推证即可.
试题解析:(1)解:∵椭圆![]() 过点
过点![]() ,∴
,∴![]() ,①………………………………1分
,①………………………………1分
∵椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点,∴
对称的图形过坐标原点,∴![]() ,………………………………2分
,………………………………2分
∵![]() ,∴
,∴![]() ,②…………………………………………………………3分
,②…………………………………………………………3分
由①②得![]() ,
,![]() ,……………………………………………………4分
,……………………………………………………4分
∴椭圆![]() 的方程为
的方程为![]() .………………………………………………5分
.………………………………………………5分
(2)证明:易知直线![]() 的斜率必存在,设直线
的斜率必存在,设直线![]() 的方程为
的方程为![]() ,
,
代入![]() 得
得![]() ,
,
由![]() 得,
得,![]() .…………………………7分
.…………………………7分
设![]() ,
,![]() ,则
,则
![]() ,
,![]() ,……………………………………8分
,……………………………………8分
则直线![]() 的方程为
的方程为![]() ,
,
令![]() 得:
得:![]()
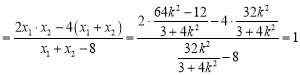 ,
,
∴直线![]() 过定点
过定点![]() ,又
,又![]() 的右焦点为
的右焦点为![]() ,∴直线
,∴直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .…………12分
.…………12分


科目:高中数学 来源: 题型:
【题目】过曲线C1:![]() -
-![]() =1(a>0,b>0)的左焦点F1作曲线C2:x2+y2=a2的切线,设切点为M,直线F1M交曲线C3:y2=2px(p>0)于点N,其中曲线C1与C3有一个共同的焦点,若|MF1|=|MN|,则曲线C1的离心率为( )
=1(a>0,b>0)的左焦点F1作曲线C2:x2+y2=a2的切线,设切点为M,直线F1M交曲线C3:y2=2px(p>0)于点N,其中曲线C1与C3有一个共同的焦点,若|MF1|=|MN|,则曲线C1的离心率为( )
A. ![]() B.
B. ![]() -1 C.
-1 C. ![]() +1 D.
+1 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() +
+![]() =1(a>b>0)的左焦点为F,右顶点为A,抛物线y2=
=1(a>b>0)的左焦点为F,右顶点为A,抛物线y2=![]() (a+c)x与椭圆交于B,C两点,若四边形ABFC是菱形,则椭圆的离心率等于( )
(a+c)x与椭圆交于B,C两点,若四边形ABFC是菱形,则椭圆的离心率等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln x+![]() +ax(a是实数),g(x)=
+ax(a是实数),g(x)=![]() +1.
+1.
(1)当a=2时,求函数f(x)在定义域上的最值;
(2)若函数f(x)在[1,+∞)上是单调函数,求a的取值范围;
(3)是否存在正实数a满足:对于任意x1∈[1,2],总存在x2∈[1,2],使得f(x1)=g(x2)成立? 若存在,求出a的取值范围,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
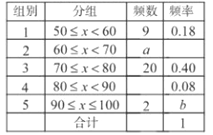

请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出![]() 的值;
的值;
(2)老师说:“小王的测试成绩是全班同学成绩的中位数”,那么小王的测试成绩在什么范围内?
(3)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用:列表法或树状图求出小明、小敏同时被选中的概率.(注:五位同学请用![]() 表示,其中小明为
表示,其中小明为![]() ,小敏为
,小敏为![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知右焦点为![]() 的椭圆
的椭圆![]() 关于直线
关于直线![]() 对称的图形过坐标原点.
对称的图形过坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且不垂直于
且不垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:直线
,证明:直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各进行3次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为![]() 求:(1)甲恰好击中目标2次的概率;(2)乙至少击中目标2次的概率;
求:(1)甲恰好击中目标2次的概率;(2)乙至少击中目标2次的概率;
(3)乙恰好比甲多击中目标2次的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,AD∥BC,AD=AB=DC=![]() BC=1,E是PC的中点,平面PAC⊥平面ABCD.
BC=1,E是PC的中点,平面PAC⊥平面ABCD.

(1)证明:ED∥平面PAB;
(2)若PC=2,PA=![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com