
分析 先求出函数f(x)的表达式,画出函数y=|f(x)|的图象,得到函数的单调区间,从而得到关于a的不等式组,解出a的范围即可.
解答 解:∵f(0)=f(2),∴对称轴x=1,
又∴二次函数f(x)的最小值为-4,
∴设函数f(x)=m(x-1)2-4,由f(0)=-3,
得:m=1,
∴f(x)=(x-1)2-4,
画出函数y=|f(x)|的图象,如图示: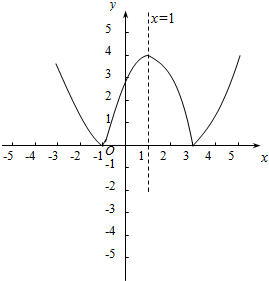 ,
,
若y=|f(x)|在区间[3a,a+1]上单调,
则$\left\{\begin{array}{l}{3a<a+1}\\{a+1≤-1}\end{array}\right.$或$\left\{\begin{array}{l}{3a<a+1}\\{3a≥-1}\\{a+1≤1}\end{array}\right.$或$\left\{\begin{array}{l}{3a<a+1}\\{3a≥1}\\{a+1≤3}\end{array}\right.$或$\left\{\begin{array}{l}{3a<a+1}\\{3a≥3}\\{a+1>3}\end{array}\right.$,
解得:a∈$(-∞,-2]∪[-\frac{1}{3},0]∪[\frac{1}{3},\frac{1}{2})$说明:端点-2,-$\frac{1}{3}$,$\frac{1}{3}$可开可闭,
故答案为:$(-∞,-2]∪[-\frac{1}{3},0]∪[\frac{1}{3},\frac{1}{2})$.
点评 本题考查了二次函数的性质,考查函数的单调性问题,考查数形结合思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -4 | C. | -1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
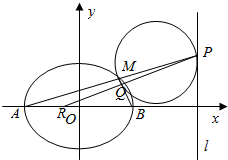 如图,AB是长轴长为6,焦距为2的椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,直线l的方程为x=9,M是椭圆C上异于A,B的一点,直线AM交l于点P.
如图,AB是长轴长为6,焦距为2的椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点,直线l的方程为x=9,M是椭圆C上异于A,B的一点,直线AM交l于点P.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
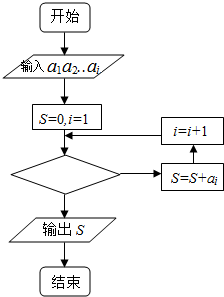 某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表所示:
某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表所示:| 队员i | 1 | 2 | 3 | 4 | 5 | 6 |
| 三分球个数ai | 9 | 13 | 11 | 7 | 5 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com