
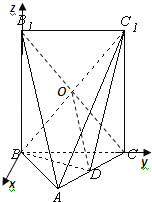
【题目】如图,五面体A﹣BCC1B1中,AB1=4.底面ABC 是正三角形,AB=2.四边形BCC1B1是矩形,二面角A﹣BC﹣C1为直二面角.
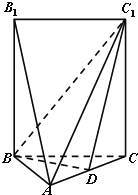
(1)D在AC上运动,当D在何处时,有AB1//平面BDC1,并且说明理由;
(2)当AB1//平面BDC1时,求二面角C﹣BC1﹣D余弦值.
【答案】(1)当D为AC中点时,有AB1//平面BDC1,理由见解析;(2)![]() .
.
【解析】
(1)根据线面平行以及中位线的性质易得当D为AC中点时,有AB1//平面BDC1,再连接B1C交BC1于O,连接DO,进而证明DO//AB1即可.
(2)以![]() 为原点建立空间直角坐标系,再分别求得面
为原点建立空间直角坐标系,再分别求得面![]() 与面
与面![]() 的法向量,继而求得二面角
的法向量,继而求得二面角![]() 的余弦值即可.
的余弦值即可.
(1)当D为AC中点时,有AB1//平面BDC1,
证明:连接B1C交BC1于O,连接DO
∵四边形BCC1B1是矩形
∴O为B1C中点又D为AC中点,从而DO//AB1,
∵AB1平面BDC1,DO平面BDC1
∴AB1//平面BDC1
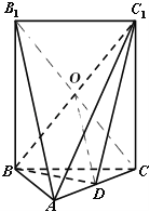
(2)建立空间直角坐标系B﹣xyz如图所示,则B(0,0,0),A(![]() ,1,0),C(0,2,0),D(
,1,0),C(0,2,0),D(![]() ,
,![]() ,0),C1(0,2,2
,0),C1(0,2,2![]() ),
),
所以![]() (
(![]() ,
,![]() ,0),
,0),![]() (0,2,2
(0,2,2![]() ).
).
设![]() 为平面BDC1的法向量,则有
为平面BDC1的法向量,则有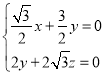 ,即
,即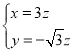
令![]() ,可得平面BDC1的一个法向量为
,可得平面BDC1的一个法向量为![]() (3,
(3,![]() ,1),
,1),
而平面BCC1的一个法向量为![]() ,
,
所以cos![]() ,
,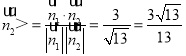 ,故二面角C﹣BC1﹣D的余弦值为
,故二面角C﹣BC1﹣D的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】为支援边远地区教育事业的发展,现有5名师范大学毕业生主动要求赴西部某地区三所不同的学校去支教,每个学校至少去1人,甲、乙不能安排在同一所学校,则不同的安排方法有( )
A.180种B.150种C.90种D.114种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,过椭圆的左、右焦点
,过椭圆的左、右焦点![]() 分别作倾斜角为
分别作倾斜角为![]() 的直线
的直线![]() ,
,![]() 分别交椭圆于A,B和C,D两点,当
分别交椭圆于A,B和C,D两点,当![]() 时,直线AB与CD之间的距离为
时,直线AB与CD之间的距离为![]() .
.
(1)求椭圆的标准方程;
(2)若AB不与x轴重合,点P在椭圆上,且满足![]() (t>0).若
(t>0).若![]() ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<![]() )的图象如图所示,为了得到g(x)=Acosωx的图象,只需把y=f(x)的图象上所有的点( )
)的图象如图所示,为了得到g(x)=Acosωx的图象,只需把y=f(x)的图象上所有的点( )
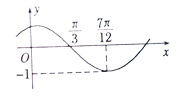
A. 向右平移![]() 个单位长度 B. 向左平移
个单位长度 B. 向左平移![]() 个单位长度
个单位长度
C. 向右平移![]() 个单位长度 D. 向左平移
个单位长度 D. 向左平移![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)试探究当![]() 时,方程
时,方程![]() 的解的个数,并说明理由.
的解的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 上顶点为A,右顶点为B,离心率
上顶点为A,右顶点为B,离心率![]() ,O为坐标原点,原点到直线AB的距离为
,O为坐标原点,原点到直线AB的距离为![]() .
.
(1)求椭圆C的标准方程;
(2)直线![]() 与椭圆C相交于E、F两不同点,若椭圆C上一点P满足
与椭圆C相交于E、F两不同点,若椭圆C上一点P满足![]() .求△EPF面积的最大值及此时的
.求△EPF面积的最大值及此时的![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某消费者协会在3月15号举行了以“携手共治,畅享消费”为主题的大型宣传咨询服务活动,着力提升消费者维权意识.组织方从参加活动的1000名群众中随机抽取n名群众,按他们的年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,其中第1组
,其中第1组![]() 有6人,得到的频率分布直方图如图所示.
有6人,得到的频率分布直方图如图所示.
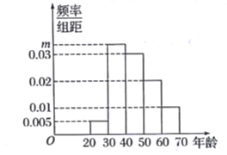
(1)求m,n的值,并估计抽取的n名群众中年龄在![]() 的人数;
的人数;
(2)已知第1组群众中男性有2人,组织方要从第1组中随机抽取3名群众组成维权志愿者服务队,求至少有两名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com