
【题目】某轮船公司的一艘轮船每小时花费的燃料费与轮船航行速度的平方成正比,比例系数为![]() 轮船的最大速度为15海里
轮船的最大速度为15海里![]() 小时
小时![]() 当船速为10海里
当船速为10海里![]() 小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元
小时,它的燃料费是每小时96元,其余航行运作费用(不论速度如何)总计是每小时150元![]() 假定运行过程中轮船以速度v匀速航行.
假定运行过程中轮船以速度v匀速航行.
![]() 求k的值;
求k的值;
![]() 求该轮船航行100海里的总费用
求该轮船航行100海里的总费用![]() 燃料费
燃料费![]() 航行运作费用
航行运作费用![]() 的最小值.
的最小值.
【答案】![]() 值为
值为![]() ,
,![]() 该轮船航行100海里的总费用W的最小值为
该轮船航行100海里的总费用W的最小值为![]() 0元
0元
【解析】
![]() 根据题意,设比例系数为k,得燃料费为
根据题意,设比例系数为k,得燃料费为![]() ,将
,将![]() 时
时![]() 代入即可算出k的值;
代入即可算出k的值;
![]() 算出航行100海里的时间为
算出航行100海里的时间为![]() 小时,可燃料费为96v,其余航行运作费用为
小时,可燃料费为96v,其余航行运作费用为![]() 元,由此可得航行100海里的总费用为
元,由此可得航行100海里的总费用为![]() ,再运用基本不等式求最值即可.
,再运用基本不等式求最值即可.
![]() 由题意,设燃料费为
由题意,设燃料费为![]() ,
,
![]() 当船速为10海里
当船速为10海里![]() 小时,它的燃料费是每小时96元,
小时,它的燃料费是每小时96元,
![]() 当
当![]() 时,
时,![]() ,可得
,可得![]() ,解之得
,解之得![]() .
.
![]() 其余航行运作费用
其余航行运作费用![]() 不论速度如何
不论速度如何![]() 总计是每小时150元.
总计是每小时150元.
![]() 航行100海里的时间为
航行100海里的时间为![]() 小时,可得其余航行运作费用为
小时,可得其余航行运作费用为![]() 元
元
因此,航行100海里的总费用为
![]()
![]() ,
,
![]() 当且仅当
当且仅当![]() 时,即
时,即![]() 时,
时,
航行100海里的总费用最小,且这个最小值为2400元.
答:![]() 值为
值为![]() ,
,![]() 该轮船航行100海里的总费用W的最小值为
该轮船航行100海里的总费用W的最小值为![]() 元
元![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
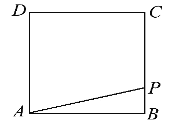
【题目】在边长为4的正方形ABCD的边上有一点P,沿着折线BCDA由点B(起点)向点A(终点)运动.设点P运动的路程为x,△APB的面积为y,且y与x之间的函数关系式用如图所示的程序框图给出.
(1)写出程序框图中①,②,③处应填充的式子.
(2)若输出的面积y值为6,则路程x的值为多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3+ax2+bx+1的导数![]() 满足
满足![]() ,
,![]() ,其中常数a,b∈R.
,其中常数a,b∈R.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)设![]() ,求函数g(x)的极值.
,求函数g(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个函数f(x),如果对任意一个三角形,只要它的三边长a,b,c都在f(x)的定义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“三角保型函数”,给出下列函数: ①f(x)= ![]() ;②f(x)=x2;③f(x)=2x;④f(x)=lgx,
;②f(x)=x2;③f(x)=2x;④f(x)=lgx,
其中是“三角保型函数”的是( )
A.①②
B.①③
C.②③④
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x=4n+1,n∈Z}B={x|x=4n﹣3,n∈z},C={x|x=8n+1,n∈z},则A,B,C的关系是( )
A.C是B的真子集、B是A的真子集
B.A是B的真子集、B是C的真子集
C.C是A的真子集、A=B
D.A=B=C
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为R,它的导函数y=f′(x)的部分图象如图所示,则下面结论正确的是( ) 
A.在(1,2)上函数f(x)为增函数
B.在(3,4)上函数f(x)为减函数
C.在(1,3)上函数f(x)有极大值
D.x=3是函数f(x)在区间[1,5]上的极小值点
查看答案和解析>>
科目:高中数学 来源: 题型:
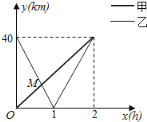
【题目】在一条笔直公路上有A,B两地,甲骑自行车从A地到B地,乙骑着摩托车从B地到A地,到达A地后立即按原路返回,如图是甲乙两人离A地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图象,根据图象解答以下问题:
之间的函数图象,根据图象解答以下问题:
![]() 直接写出
直接写出![]() ,
,![]() 与x之间的函数关系式
与x之间的函数关系式![]() 不必写过程
不必写过程![]() ,求出点M的坐标,并解释该点坐标所表示的实际意义;
,求出点M的坐标,并解释该点坐标所表示的实际意义;
![]() 若两人之间的距离不超过5km时,能够用无线对讲机保持联系,求在乙返回过程中有多少分钟甲乙两人能够用无线对讲机保持联系;
若两人之间的距离不超过5km时,能够用无线对讲机保持联系,求在乙返回过程中有多少分钟甲乙两人能够用无线对讲机保持联系;
![]() 若甲乙两人离A地的距离之积为
若甲乙两人离A地的距离之积为![]() ,求出函数
,求出函数![]() 的表达式,并求出它的最大值.
的表达式,并求出它的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com