
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c且acosB=4,bsinA=3.
(1)求tanB及边长a的值;
(2)若△ABC的面积S=9,求△ABC的周长.
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB、PB的中点 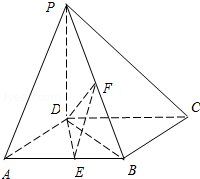
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论;
(3)求DB与平面DEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左右顶点分别为A,B,点P为椭圆上异于A,B的任意一点.
的左右顶点分别为A,B,点P为椭圆上异于A,B的任意一点.
(Ⅰ)求直线PA与PB的斜率之积;
(Ⅱ)过点 ![]() 作与x轴不重合的任意直线交椭圆E于M,N两点.证明:以MN为直径的圆恒过点A.
作与x轴不重合的任意直线交椭圆E于M,N两点.证明:以MN为直径的圆恒过点A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)已知ABCD是复平面内的平行四边形,并且A,B,C三点对应的复数分别是3+i,﹣2i,﹣1﹣i,求D点对应的复数;
(2)已知复数Z1=2, ![]() =i,并且|z|=2
=i,并且|z|=2 ![]() ,|z﹣z1|=|z﹣z2|,求z.
,|z﹣z1|=|z﹣z2|,求z.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点H(x0 , y0)在圆C:x2+y2+Dx+Ey+F=0(其中点C为圆心,D2+E2﹣4F>0)外,由点H向圆C引切线,其中一个切点为M.
求证:|HM|= ![]() ;
;
(1)已知点H(x0 , y0)在圆C:x2+y2+Dx+Ey+F=0(其中点C为圆心,D2+E2﹣4F>0)外,由点H向圆C引切线,其中一个切点为M.
求证:|HM|= ![]() ;
;
(2)如图,P是直线x=4上一动点,以P为圆心的圆P经定点B(1,0),直线l是圆P在点B处的切线,过A(﹣1,0)作圆P的两条切线分别与l交于E,F两点.
求证:|EA|+|EB|为定值.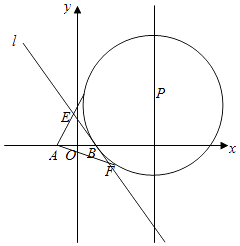
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x,y满足约束条件 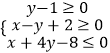 ,且目标函数z=ax+y仅在点(4,1)处取得最大值,则原点O到直线ax﹣y+17=0的距离d的取值范围是( )
,且目标函数z=ax+y仅在点(4,1)处取得最大值,则原点O到直线ax﹣y+17=0的距离d的取值范围是( )
A.(4 ![]() ,17]
,17]
B.(0,4 ![]() )
)
C.( ![]() ,17]
,17]
D.(0, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:
①对立事件一定是互斥事件;
②函数y=x+ ![]() 的最小值为2;
的最小值为2;
③八位二进制数能表示的最大十进制数为256;
④在△ABC中,若a=80,b=150,A=30°,则该三角形有两解.
其中正确命题的个数为( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD的平行四边形,∠ADC=60°, ![]() ,PA⊥面ABCD,E为PD的中点.
,PA⊥面ABCD,E为PD的中点.
(Ⅰ)求证:AB⊥PC
(Ⅱ)若PA=AB= ![]() ,求三棱锥P﹣AEC的体积.
,求三棱锥P﹣AEC的体积.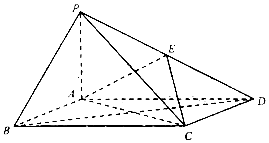
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com