
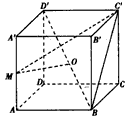
| (Ⅰ)证明:连结AC,取AC的中点K,则K为BD的中点,连结OK, 因为点M是棱AA′的中点,点D是BD′的中点, 所以 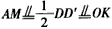 ,所以 ,所以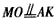 , ,由AA′⊥AK,得MO⊥AA′, 因为AK⊥BD,AK⊥BB′, 所以AK⊥平面BDD′B′, 所以AK⊥BD′,所以MO⊥BD′, 又因为OM与异面直线AA′和BD′都相交, 故OM为异面直线AA′和BD′的公垂线. (Ⅱ)解:取BB′的中点N,连结MN,则MN⊥平面BCC′B′, 过点N作NH⊥BC′于H,连结MH,则由三垂线定理得,BC′⊥MH, 从而,∠MHN为二面角M-BC′-B′的平面角, 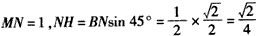 , ,在Rt△MNH中,  , ,故二面角M-BC′-B′的大小为 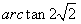 。 。(Ⅲ)解:易知,S△OBC=S△OA′D′,且△OBC和△OA′D′都在平面BCD′A′内, 点O到平面MA′D′的距离 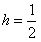 , ,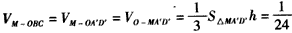 。 。 |
 |


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com