
【题目】已知函数![]()
![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,求证:
时,求证: ![]() .
.
【答案】(1)答案见解析;(2)证明见解析.
【解析】试题分析:
(1)函数![]() 的定义域为
的定义域为![]() ,且
,且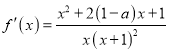 .原问题转化为考查二次函数
.原问题转化为考查二次函数![]() 的性质可得:
的性质可得:
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间,
,无单调递减区间,
当![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)当![]() 时,原问题等价于
时,原问题等价于![]() .构造函数
.构造函数![]() ,则
,则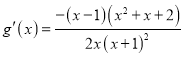 .结合导函数的性质可知当
.结合导函数的性质可知当![]() 时,
时, ![]() 取得最大值,即
取得最大值,即![]() ,
, ![]() 成立.
成立.
试题解析:
(1)![]() 的定义域为
的定义域为![]() ,
, 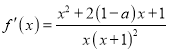 .
.
考虑![]() .
.
①当![]() ,即
,即![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() ,即
,即![]() 或
或![]() 时,由
时,由![]() 得
得![]() .
.
若![]() ,则
,则![]() 恒成立,此时
恒成立,此时![]() 在
在![]() 上单调递增;
上单调递增;
若![]() ,则
,则![]() ,
,
此时![]() 或
或![]() ;
;
![]() .
.
综上,当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间,
,无单调递减区间,
当![]() 时,
时, ![]() 的单调递增区间为
的单调递增区间为![]() ,
,
单调递减区间为![]() .
.
(2)当![]() 时,
时, ![]() .
.
令![]() ,
,
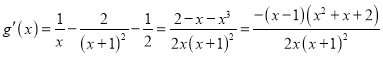 .
.
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,即当
上单调递减,即当![]() 时,
时, ![]() 取得最大值,
取得最大值,
故![]() ,即
,即![]() 成立,得证.
成立,得证.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源: 题型:
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力,某移动支付公司在我市随机抽取了100名移动支付用户进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)如果认为每周使用移动支付超过3次的用户“喜欢使用移动支付”,能否在犯错误概率不超过![]() 的前提下,认为是否“喜欢使用移动支付”与性别有关?
的前提下,认为是否“喜欢使用移动支付”与性别有关?
(2)每周使用移动支付6次及6次以上的用户称为“移动支付达人”,视频率为概率,在我市所有“移动支付达人”中,随机抽取4名用户,
①求抽取的4名用户中,既有男“移动支付达人”又有女“移动支付达人”的概率;
②为了鼓励女性用户使用移动支付,对抽出的女“移动支付达人”每人奖励500元,记奖励总金额为![]() ,求
,求![]() 的数学期望.
的数学期望.
附表及公式:
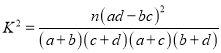
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.
(1)求角A的值;
(2)若![]() ,
, ![]() ,求△ABC的面积S.
,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥S﹣ABCD中,底面ABCD是边长为4的菱形,∠BAD=60°,SA=SD=2![]() ,点E是棱AD的中点,点F在棱SC上,且
,点E是棱AD的中点,点F在棱SC上,且![]() λ,SA//平面BEF.
λ,SA//平面BEF.
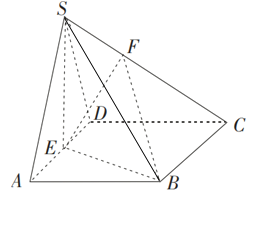
(1)求实数λ的值;
(2)求三棱锥F﹣EBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
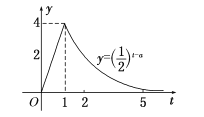
(1)写出第一次服药后,y与t之间的函数关系式y=f(t);
(2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗有效.求服药一次后治疗有效的时间是多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后,所得图象对应的函数为
个单位后,所得图象对应的函数为![]() .若关于
.若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实根,求实数
上有两个不相等的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)在y=x2的函数图象上.
(1)求数列{an}的通项公式;
(2)若bn=(-1)n+1anan+1,求数列{bn}的前100项和T100.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com