
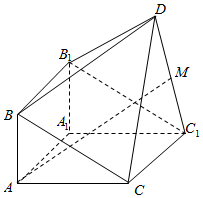
 ��ͼ����ֱ������ABC-A1B1C1������D-BB1C1C���ɵļ������У���BAC=90�㣬AB=1��BC=BB1=2��C1D=CD=$\sqrt{5}$��ƽ��CC1D��ƽ��ACC1A1��
��ͼ����ֱ������ABC-A1B1C1������D-BB1C1C���ɵļ������У���BAC=90�㣬AB=1��BC=BB1=2��C1D=CD=$\sqrt{5}$��ƽ��CC1D��ƽ��ACC1A1������ ����֤��AC��CC1���õ�AC��ƽ��CC1D������֤��AC��DC1��
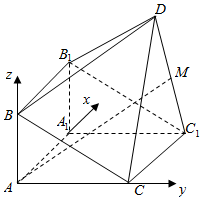
�����á�BAC=90�㣬�����ռ�ֱ������ϵA-xyz��
������֪�����ɵ�A��0��0��0����$C��0��\sqrt{3}��0��$��${C_1}��2��\sqrt{3}��0��$��B��0��0��1����B1��2��0��1����$D��1��\sqrt{3}��2��$��
�����������AM��ƽ��DBB1���ɽ�Ϊ0����AM��ƽ��DBB1��
���������������
���  �⣺����֤������ֱ������ABC-A1B1C1�У�CC1��ƽ��ABC����AC��CC1��
�⣺����֤������ֱ������ABC-A1B1C1�У�CC1��ƽ��ABC����AC��CC1��
��ƽ��CC1D��ƽ��ACC1A1����ƽ��CC1D��ƽ��ACC1A1=CC1��
����AC��ƽ��CC1D��
��C1D?ƽ��CC1D������AC��DC1��
����֤������ֱ������ABC-A1B1C1�У�AA1��ƽ��ABC��
����AA1��AB��AA1��AC��
�֡�BAC=90�㣬���ԣ���ͼ�����ռ�ֱ������ϵA-xyz��
������֪�����ɵ�A��0��0��0����$C��0��\sqrt{3}��0��$��${C_1}��2��\sqrt{3}��0��$��B��0��0��1����B1��2��0��1����$D��1��\sqrt{3}��2��$��
����$\overrightarrow{B{B_1}}=��2��0��0��$��$\overrightarrow{BD}=��1��\sqrt{3}��1��$��
��ƽ��DBB1�ķ�����Ϊ$\overrightarrow n=��x��y��z��$��
��$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{B{B_1}}=0\\ \overrightarrow n•\overrightarrow{BD}=0\end{array}\right.$��$\left\{\begin{array}{l}2x=0\\ x+\sqrt{3}y+z=0\end{array}\right.$
��y=1����$z=-\sqrt{3}$��x=0������$\overrightarrow n=��0��1��-\sqrt{3}��$��
��ΪMΪDC1�е㣬����$M��\frac{3}{2}��\sqrt{3}��1��$������$\overrightarrow{AM}=��\frac{3}{2}��\sqrt{3}��1��$��
��$\overrightarrow{AM}•\overrightarrow n=��\frac{3}{2}��\sqrt{3}��1��•��0��1��-\sqrt{3}��=0$���ɵ�$\overrightarrow{AM}��\overrightarrow n$��
����AM��ƽ��DBB1���ɽ�Ϊ0��
��AM��ƽ��DBB1��
���⣺�ɣ���֪ƽ��BB1D�ķ�����Ϊ$\overrightarrow n=��0��1��-\sqrt{3}��$��
��$\overrightarrow{BP}=��\overrightarrow{BC}$���ˡ�[0��1]��
��$P��0��\sqrt{3}�ˣ�1-�ˣ�$��$\overrightarrow{DP}=��-1��\sqrt{3}��-\sqrt{3}��-1-�ˣ�$��
��ֱ��DP��ƽ��DBB1�ɽ�Ϊ$\frac{��}{3}$����$|cos��\overrightarrow n��\overrightarrow{DP}��|=\frac{{|\overrightarrow n•\overrightarrow{DP}|}}{{|\overrightarrow n|•|\overrightarrow{DP}|}}=\frac{{|2\sqrt{3}��|}}{{2\sqrt{4{��^2}-4��+5}}}=\frac{{\sqrt{3}}}{2}$��
���$��=\frac{5}{4}∉[{0��1}]$��
�ʲ����������ĵ㣮
���� ���⿼���˿ռ����ߴ�ֱ������ƽ�е��ж��������������ǣ������е���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �ɡ������Ρ� | ���ɡ������Ρ� | �ϼ� | |
| ���� | 30 | ||
| �� | 10 | ||
| �ϼ� | 100 |
| P��K2��k�� | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2+b2��0 | B�� | ab=0 | C�� | a=0��b��0 | D�� | a��0��b=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3��2 | B�� | 2 | C�� | -2��3 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{2\sqrt{3}}}{3}$ | B�� | $\frac{\sqrt{3}}{3}$ | C�� | $\sqrt{3}$ | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | $\sqrt{5}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com