
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.

(1)求A;
(2)若AD为BC边上的中线,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】(1)A=60°;(2)![]()
【解析】
(1)利用正弦定理,把边化为角,结合辅助角公式可求;
(2)利用三角形内角关系求出![]() ,结合正弦定理求出
,结合正弦定理求出![]() 关系,利用余弦定理可求
关系,利用余弦定理可求![]() .
.
(1)acos C+![]() asin C-b-c=0,由正弦定理得sin Acos C+
asin C-b-c=0,由正弦定理得sin Acos C+![]() sin Asin C=sin B+sin C,
sin Asin C=sin B+sin C,
即sin Acos C+![]() sin Asin C=sin(A+C)+sin C,
sin Asin C=sin(A+C)+sin C,
又sin C≠0,所以化简得![]() sin A-cos A=1,所以sin(A-30°)=
sin A-cos A=1,所以sin(A-30°)=![]() .
.
在△ABC中,0°<A<180°,所以A-30°=30°,得A=60°.
(2)在△ABC中,因为cos B=![]() ,所以sin B=
,所以sin B=![]() .
.
所以sin C=sin(A+B)=![]() ×
×![]() +
+![]() ×
×![]() =
=![]() .
.
由正弦定理得,![]() .
.
设a=7x,c=5x(x>0),则在△ABD中,AD2=AB2+BD2-2AB·BDcos B,
即![]() =25x2+
=25x2+![]() ×49x2-2×5x×
×49x2-2×5x×![]() ×7x×
×7x×![]() ,解得x=1,所以a=7,c=5,
,解得x=1,所以a=7,c=5,
故S△ABC=![]() acsin B=10
acsin B=10![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
,![]() ,上下顶点分别为
,上下顶点分别为![]() ,
,![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,离心率为e.
,离心率为e.
(1)若![]() ,设四边形
,设四边形![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,且
,且 ,求椭圆C的方程;
,求椭圆C的方程;
(2)若![]() ,设直线
,设直线![]() 与椭圆C相交于P,Q两点,
与椭圆C相交于P,Q两点,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,坐标原点O在以MN为直径的圆上,且
的中点,坐标原点O在以MN为直径的圆上,且![]() ,求实数k的取值范围.
,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个命题与自然数n有关,如果当![]() (
(![]() )时该命题成立,则可得
)时该命题成立,则可得![]() 时该命题也成立,若已知
时该命题也成立,若已知![]() 时命题不成立,则下列说法正确的是______(填序号)
时命题不成立,则下列说法正确的是______(填序号)
(1)![]() 时,该命题不成立;
时,该命题不成立;
(2)![]() 时,该命题不成立;
时,该命题不成立;
(3)![]() 时,该命题可能成立;
时,该命题可能成立;
(4)![]() 时,该命题可能成立也可能不成立,但若
时,该命题可能成立也可能不成立,但若![]() 时命题成立,则对任意
时命题成立,则对任意![]() ,该命题都成立.
,该命题都成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中真命题是![]()
![]()
A. 同垂直于一直线的两条直线互相平行
B. 底面各边相等,侧面都是矩形的四棱柱是正四棱柱
C. 过空间任一点与两条异面直线都垂直的直线有且只有一条
D. 过球面上任意两点的大圆有且只有一个
查看答案和解析>>
科目:高中数学 来源: 题型:
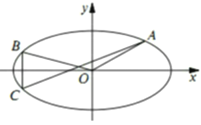
【题目】如图,已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(I)求椭圆![]() 的标准方程;
的标准方程;
(II)设点![]() ,
,![]() 是椭圆
是椭圆![]() 上异于顶点的任意两点,直线
上异于顶点的任意两点,直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() 且
且![]() .
.
①求![]() 的值;
的值;
②设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,试求直线
,试求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,已知椭圆 C:![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,且过点
,且过点![]() ,点P在第四象限, A为左顶点, B为上顶点, PA交y轴于点C,PB交x轴于点D.
,点P在第四象限, A为左顶点, B为上顶点, PA交y轴于点C,PB交x轴于点D.
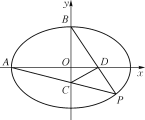
(1) 求椭圆 C 的标准方程;
(2) 求 △PCD 面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长为![]() ,宽为
,宽为![]() 的矩形纸片
的矩形纸片![]() 中,
中,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转
翻转![]() (
(![]() 平面
平面![]() ),若
),若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻转过程中,下列说法错误的是( )
翻转过程中,下列说法错误的是( )

A. ![]() 平面
平面![]()
B. 异面直线![]() 与
与![]() 所成角是定值
所成角是定值
C. 三棱锥![]() 体积的最大值是
体积的最大值是![]()
D. 一定存在某个位置,使![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com