
 ~
~ ,又
,又 ,则
,则 和
和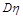 的值分别是( )
的值分别是( )A. 和 和 | B. 和 和 | C. 和 和 | D. 和 和 |
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源:不详 题型:解答题
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求 的分布列和数学期望。
的分布列和数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,中奖后电信公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为X(元).
,中奖后电信公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为X(元).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com