
已知圆 内一点
内一点 过点
过点 的直线
的直线 交圆
交圆 于
于 两点,且满足
两点,且满足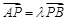 (
( 为参数).
为参数).
(1)若 ,求直线
,求直线 的方程;
的方程;
(2)若 求直线
求直线 的方程;
的方程;
(3)求实数 的取值范围.
的取值范围.
(1)  或
或 (2)
(2)  (3)
(3) 
解析试题分析:(1)当直线 的斜率不存在时,
的斜率不存在时,  ,不满足,故可设所求直线
,不满足,故可设所求直线 的方程为
的方程为 ,代入圆的方程,整理得
,代入圆的方程,整理得 ,利用弦长公式可求得直线方程为
,利用弦长公式可求得直线方程为 或
或 .
.
(2)当直线 的斜率不存在时,
的斜率不存在时,  或
或 ,不满足,故可设所求直线
,不满足,故可设所求直线 的方程为
的方程为 ,代入圆的方程,整理得
,代入圆的方程,整理得 ,(*)设
,(*)设 ,则
,则 为方程(*)的两根,由
为方程(*)的两根,由 可得
可得 ,则有
,则有 ,
, 得
得 ,解得
,解得 ,所以直线
,所以直线 的方程为
的方程为
(3)当直线 的斜率不存在时,
的斜率不存在时,  或
或 ,
, 或
或 ,当直线
,当直线 的斜率存在时可设所求直线
的斜率存在时可设所求直线 的方程为
的方程为 ,代入圆的方程,整理得
,代入圆的方程,整理得 ,(*)设
,(*)设 ,则
,则 为方程(*)的两根,由
为方程(*)的两根,由 可得
可得 ,则有
,则有 ,
, 得
得 ,而
,而 ,由
,由 可解得
可解得 ,所以实数
,所以实数 的取值范围为
的取值范围为 -
-
考点:本题考查了直线与圆的位置关系
点评:平面解析几何里解决直线与圆的位置关系有以下两种方法:一是联立直线和圆组成方程组,若方程组有两组解,则说明直线与圆相交;若只有一组解,则说明直线与圆相切;若无解,则直线与圆相离.二是看圆心到直线距离d与圆半径r大小,若d>r,则直线与圆相离;若d<r,则直线与圆相交;若d=r,则直线与圆相切.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
在平面直角坐标系 中,已知圆
中,已知圆 的圆心为
的圆心为 ,过点
,过点 且斜率为
且斜率为 的直线与圆
的直线与圆 相交于不同的两点
相交于不同的两点 .
.
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)以OA,OB为邻边作平行四边形OADB,是否存在常数 ,使得直线OD与PQ平行?如果存在,求
,使得直线OD与PQ平行?如果存在,求 值;如果不存在,请说明理由.
值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
若圆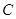 经过坐标原点和点
经过坐标原点和点 ,且与直线
,且与直线 相切, 从圆
相切, 从圆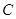 外一点
外一点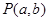 向该圆引切线
向该圆引切线 ,
, 为切点,
为切点,
(Ⅰ)求圆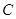 的方程;
的方程;
(Ⅱ)已知点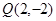 ,且
,且 , 试判断点
, 试判断点 是否总在某一定直线
是否总在某一定直线 上,若是,求出
上,若是,求出 的方程;若不是,请说明理由;
的方程;若不是,请说明理由;
(Ⅲ)若(Ⅱ)中直线 与
与 轴的交点为
轴的交点为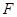 ,点
,点 是直线
是直线 上两动点,且以
上两动点,且以 为直径的圆
为直径的圆 过点
过点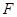 ,圆
,圆 是否过定点?证明你的结论.
是否过定点?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com