
����Ŀ��ijУѧ���о�ѧϰС�鷢�֣�ѧ���Ͽε�ע����ָ����������ʱ��ı仯���仯����ʦ���ο�ʼʱ��ѧ������Ȥ������������ѧ������Ȥ�����ֽ������״̬һ��ʱ�䣬���ѧ����ע������ʼ��ɢ����![]() ��ʾѧ��ע����ָ�꣮
��ʾѧ��ע����ָ�꣮
��С�鷢��![]() ��ʱ��
��ʱ��![]() �����ӣ��ı仯���ɣ�
�����ӣ��ı仯���ɣ�![]() Խ����ѧ����ע����Խ���У����£�
Խ����ѧ����ע����Խ���У����£�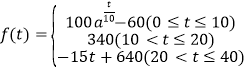 ��
��![]() ��
��![]() ����
����
���Ͽκ��![]() ����ʱ��ע����ָ��Ϊ
����ʱ��ע����ָ��Ϊ![]() ���ش��������⣺
���ش��������⣺
��![]() ����
����![]() ��ֵ��
��ֵ��
��![]() ���Ͽκ��
���Ͽκ��![]() ���Ӻ��¿�ǰ
���Ӻ��¿�ǰ![]() ���ӱȽϣ��ĸ�ʱ��ע���������У�����˵�����ɣ�
���ӱȽϣ��ĸ�ʱ��ע���������У�����˵�����ɣ�
��![]() ����һ�ڿ��У�ѧ����ע����ָ�����ٴﵽ
����һ�ڿ��У�ѧ����ע����ָ�����ٴﵽ![]() ��ʱ���ܱ��ֶ��
��ʱ���ܱ��ֶ��
���𰸡�(1) ![]() .
.
(2) �Ͽκ��![]() ����ʱ���¿�ǰ
����ʱ���¿�ǰ![]() ����ʱע���������У����ɼ�����.
����ʱע���������У����ɼ�����.
(3) ѧ����ע����ָ�����ٴﵽ![]() ��ʱ���ܱ���
��ʱ���ܱ���![]() ���ӣ�
���ӣ�
����������������1����������![]() ���Ӷ����a��ֵ��
���Ӷ����a��ֵ��
��2���Ͽκ��5����ĩʱ��![]() ���¿�ǰ5����ĩ
���¿�ǰ5����ĩ![]() ���Ӷ��ɵô𰸣�
���Ӷ��ɵô𰸣�
��3���ֱ��������κ�����![]() ���Ӷ����
���Ӷ����![]() �Ľ⣬�Ӷ�����һ�ڿ��У�ѧ����ע����ָ�����ٴﵽ140��ʱ���ܱ��ֵ�ʱ��.
�Ľ⣬�Ӷ�����һ�ڿ��У�ѧ����ע����ָ�����ٴﵽ140��ʱ���ܱ��ֵ�ʱ��.
�������![]() ����������
��������ã���![]() ʱ��
ʱ��![]() ����
����![]() ��
��
���![]() ��
��
��![]() ����
����![]() ��
��![]() ��
��
��![]() ��
��
���Ͽκ��![]() ����ʱ���¿�ǰ
����ʱ���¿�ǰ![]() ����ʱע���������У�
����ʱע���������У�
��![]() ���ٵ�
���ٵ�![]() ʱ���ɣ�
ʱ���ɣ�![]() ��֪��
��֪��![]() �����
�����![]() ��
��
�ڵ�![]() ʱ��
ʱ��![]() �������
�������
�۵�![]() ʱ��
ʱ��![]() �����
�����![]() ��
��
����������![]() ��
��
��ѧ����ע����ָ�����ٴﵽ![]() ��ʱ���ܱ���
��ʱ���ܱ���![]() ���ӣ�
���ӣ�


 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ȵĵȲ�����{an}��ǰn���ΪSn��S10=45����a3,a5,a9ǡΪ�ȱ�����{bn}��ǰ�����![]() ��
��
(1)�ֱ�������{an}��{bn}��ͨ�ʽ��
(2)��m=17����cnȡ����Сֵʱn��ֵ��
(3)��c1Ϊ����{cn}����С��ʱ�� ![]() ����Ӧ�Ŀ�ȡֵ�����ǰ�����am�ĺͼ�ΪA1��������ciΪ����
����Ӧ�Ŀ�ȡֵ�����ǰ�����am�ĺͼ�ΪA1��������ciΪ����![]() ����С��ʱ��
����С��ʱ��![]() ����Ӧ�Ŀ�ȡֵ�����ǰ�����am�ĺͼ�ΪAi��������Tn= A1+ A2+��+An����Tn.
����Ӧ�Ŀ�ȡֵ�����ǰ�����am�ĺͼ�ΪAi��������Tn= A1+ A2+��+An����Tn.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �ǹ��Ϊ��ĵȲ�����,
�ǹ��Ϊ��ĵȲ�����, ![]() �ǵȱ�����,��
�ǵȱ�����,��![]() ,
,![]() ,
,![]() .
.
(1)������![]() ,
,![]() ��ͨ�ʽ��
��ͨ�ʽ��
(2)��![]() ,������
,������![]() ��ǰ
��ǰ![]() ���
���![]() ��
��
(3)�����㲻��ʽ![]() ������
������![]() ǡ��
ǡ��![]() ��,��������
��,��������![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �Ƕ�����
�Ƕ�����![]() �ϵ��溯������
�ϵ��溯������![]() ����
����![]() ��
��![]() ʱ����
ʱ����![]() .
.
��1��֤��![]() ��
��![]() ������������
������������
��2���ⲻ��ʽ![]() ��
��
��3����![]() ��
��![]() ��
��![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Բ![]() ������
������![]() ��������
��������![]() ��ֱ��
��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() .
.
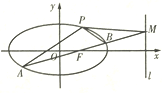
![]() ����Բ
����Բ![]() �ķ��̣�
�ķ��̣�
![]()
![]() �Ǿ����ҽ���
�Ǿ����ҽ���![]() ����һ�ң���������
����һ�ң���������![]() ������ֱ��
������ֱ��![]() ��ֱ��
��ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��
�� ![]() ��
�� ![]() ��б��Ϊ
��б��Ϊ![]() ��
�� ![]() ��
�� ![]() .�ʣ��Ƿ���ڳ���
.�ʣ��Ƿ���ڳ���![]() ��ʹ��
��ʹ��![]() �������ڣ���
�������ڣ���![]() ��ֵ���������ڣ�˵������.
��ֵ���������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x��a|+|x+5��a|
��1��������ʽf��x����|x��a|��2�Ľ⼯Ϊ[��5����1]����ʵ��a��ֵ��
��2����x0��R��ʹ��f��x0����4m+m2 �� ��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn�����Sn����Sn![]() =1��n��N��������{bn}�ǹ���d������0�ĵȲ����У������㣺b1=
=1��n��N��������{bn}�ǹ���d������0�ĵȲ����У������㣺b1=![]() ����b2��b5��ba14�ɵȱ����У�
����b2��b5��ba14�ɵȱ����У�
��1��������{an}��{bn}��ͨ�ʽ��
��2����cn=anbn��������{cn}��ǰn���Tn��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ��
��![]() ��
��![]() ��������
��������![]() �ضԽ���
�ضԽ���![]() ���𣬵õ�����
���𣬵õ�����![]() ����
����![]() ����
����![]() ���е㣬
���е㣬![]() ��
��
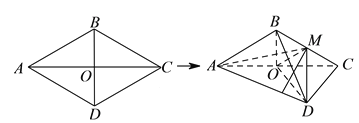
��![]() ����֤��
����֤��![]() ƽ��
ƽ��![]() ��
��
��![]() ����֤��ƽ��
����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��![]() ��������
��������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������dz��н�ͨ��һ�������ķ羰,�����Ƕ̾�����д����˺ܴ�ķ���.ijУ���������š���![]() ��������
��������![]() �����������������Ⱥ�����ȡ
�����������������Ⱥ�����ȡ![]() �˵���,�����ߵ������������ͼ��ʾ��
�˵���,�����ߵ������������ͼ��ʾ��
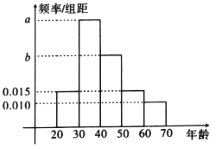
��1����֪![]() ����ε�����������
����ε�����������![]() ��������ε�����֮�ͣ�������������������Ⱥ�����g����λ����
��������ε�����֮�ͣ�������������������Ⱥ�����g����λ����
��2����![]() �������������������������а�
�������������������������а�![]() �ı����÷ֲ�����ķ�����ȡ
�ı����÷ֲ�����ķ�����ȡ![]() ��,������ѡ
��,������ѡ![]() ��,�����˶���
��,�����˶���![]() )�ĸ���.
)�ĸ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com