
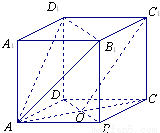
 证明:(1)连接A1C1交B1D1于O1,连接AO1.
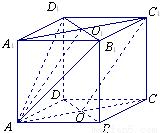
证明:(1)连接A1C1交B1D1于O1,连接AO1.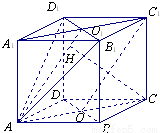 ∵平面AB1D1⊥平面ACC1A1 ,平面AB1D1∩平面ACC1A1=AO1 ,
∵平面AB1D1⊥平面ACC1A1 ,平面AB1D1∩平面ACC1A1=AO1 ,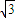 .-------------------------------12分
.-------------------------------12分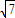
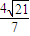 ∴sin∠CAH=
∴sin∠CAH=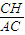 =
=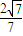 .---14分
.---14分

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
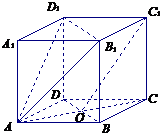 在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.
在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.查看答案和解析>>
科目:高中数学 来源: 题型:
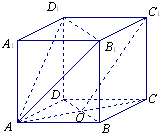 在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.
在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.查看答案和解析>>
科目:高中数学 来源: 题型:
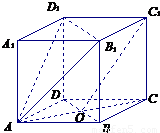
 在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.
在直平行六面体AC1中,ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1.查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省宜昌一中高三(上)10月月考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com