
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,圆
,圆![]() .
.
(1)求![]() 的取值范围,并求出圆心坐标;
的取值范围,并求出圆心坐标;
(2)有一动圆![]() 的半径为
的半径为![]() ,圆心在
,圆心在![]() 上,若动圆
上,若动圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】近年来,随着网络的普及,数码产品早已走进千家万户的生活,为了节约资源,促进资源循环利用,折旧产品回收行业得到迅猛发展,电脑使用时间越长,回收价值越低,某二手电脑交易市场对2018年回收的折旧电脑交易前使用的时间进行了统计,得到如图所示的频率分布直方图,在如图对时间使用的分组中,将使用时间落入各组的频率视为概率.

(1)若在该市场随机选取1个2018年成交的二手电脑,求其使用时间在![]() 上的概率;
上的概率;
(2)根据电脑交易市场往年的数据,得到如图所示的散点图及一些统计量的值,其中![]() (单位:年)表示折旧电脑的使用时间,
(单位:年)表示折旧电脑的使用时间,![]() (单位:百元)表示相应的折旧电脑的平均交易价格.
(单位:百元)表示相应的折旧电脑的平均交易价格.

由散点图判断,可采用![]() 作为该交易市场折旧电脑平均交易价格与使用年限
作为该交易市场折旧电脑平均交易价格与使用年限![]() 的回归方程,若
的回归方程,若![]() ,
,![]() ,选用如下参考数据,求
,选用如下参考数据,求![]() 关于
关于![]() 的回归方程,并预测在区间
的回归方程,并预测在区间![]() (用时间组的区间中点值代表该组的值)上折旧电脑的价格.
(用时间组的区间中点值代表该组的值)上折旧电脑的价格.
|
|
|
|
|
|
5.5 | 8.5 | 1.9 | 301.4 | 79.75 | 385 |
附:参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .参考数据:
.参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
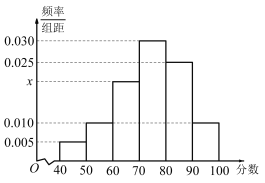
【题目】某校学生社团组织活动丰富,学生会为了解同学对社团活动的满意程度,随机选取了100位同学进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的中位数;
(3)现从被调查的问卷满意度评分值在[60,80)的学生中按分层抽样的方法抽取5人进行座谈了解,再从这5人中随机抽取2人作主题发言,求抽取的2人恰在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,直线
,直线![]() 与E交于A、B两点,且
与E交于A、B两点,且![]() ,其中O为原点.
,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为![]() ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为![]() ,证明:
,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,a1=﹣1,b1=1,a2+b2=2.
(1)若a3+b3=5,求{bn}的通项公式;
(2)若T3=21,求S3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() 交曲线
交曲线![]() 于点
于点![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 过线段
过线段![]() 的中点
的中点![]() 且与曲线
且与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的参数方程;
的参数方程;
(2)当直线![]() 倾斜角
倾斜角![]() 为何值时,
为何值时,![]() 取最小值,并求出
取最小值,并求出![]() 最小值.
最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() ,
,![]() 为椭圆
为椭圆![]() 的左顶点,
的左顶点,![]() ,
,![]() 为椭圆
为椭圆![]() 上异于
上异于![]() 的两个动点,直线
的两个动点,直线![]() ,
,![]() 与直线
与直线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 与
与![]() 的面积之比为
的面积之比为![]() ,求
,求![]() 的坐标;
的坐标;
(3)设直线与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,
,![]() ,
,![]() 三点共线,判断
三点共线,判断![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com