
【题目】已知函数![]() .
.
(1)若函数![]() 和函数
和函数![]() 在区间
在区间![]() 上均为增函数,求实数
上均为增函数,求实数![]() 的取值范围;
的取值范围;
(2)若方程![]() 有唯一解,求实数
有唯一解,求实数![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由已知中函数f(x)=x2-8lnx,g(x)=-x2+14x的解析式,我们易求出他们导函数的解析式,进而求出导函数大于0的区间,构造关于a的不等式,即可得到实数a的取值范围;(2)若方程f(x)=g(x)+m有唯一解,则函数h(x)=f(x)-g(x)=2x2-8lnx-14x与y=m的图象有且只有一个交点,求出h'(x)后,易求出函数的最值,分析函数的性质后,即可得到满足条件的实数m的值.
试题解析:(1)因为![]()
![]() ,
,
故当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
要使![]() 在
在![]() 上递增,必须
上递增,必须![]() ,
,
因为![]() ,
,
要使![]() 在
在![]() 上递增,必须
上递增,必须![]() ,即
,即![]() ,
,
由上得出,当![]() 时,
时, ![]() 在
在![]() 上均为增函数.
上均为增函数.
(2)方程![]() 有唯一解
有唯一解![]() 有唯一解,
有唯一解,
设![]() ,
,
所以![]()
![]()
![]() 随
随![]() 变化如下表:
变化如下表:
|
| 4 |
|
| - | 0 | + |
| 递减 | 极小值 | 递增 |
由于在![]() 上,
上, ![]() 只有一个极小值,所以
只有一个极小值,所以![]() 的最小值为
的最小值为![]() ,故当
,故当![]() 时,方程
时,方程![]() 有唯一解.
有唯一解.


科目:高中数学 来源: 题型:
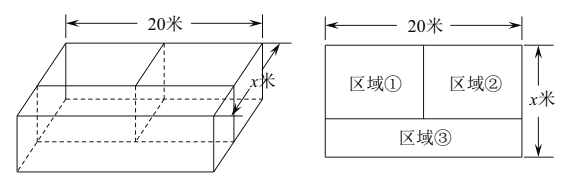
【题目】某水产养殖户制作一体积为![]() 立方米的养殖网箱(无盖),网箱内部被隔成体积相等的三块长方体区域(如图),网箱.上底面的一边长为
立方米的养殖网箱(无盖),网箱内部被隔成体积相等的三块长方体区域(如图),网箱.上底面的一边长为![]() 米,网箱的四周与隔栏的制作价格是
米,网箱的四周与隔栏的制作价格是![]() 元/平方米,网箱底部的制作价格为
元/平方米,网箱底部的制作价格为![]() 元/平方米.设网箱上底面的另一边长为
元/平方米.设网箱上底面的另一边长为![]() 米,网箱的制作总费用为
米,网箱的制作总费用为![]() 元.
元.
(1)求出![]() 与
与![]() 之间的函数关系,并指出定义域;
之间的函数关系,并指出定义域;
(2)当网箱上底面的另一边长![]() 为多少米时,制作网箱的总费用最少.
为多少米时,制作网箱的总费用最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1的方程为3x+4y﹣12=0.
(1)若直线l2与l1平行,且过点(﹣1,3),求直线l2的方程;
(2)若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点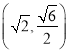 与点
与点![]() 都在椭圆
都在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 的左焦点、左顶点分别为
的左焦点、左顶点分别为![]() ,则是否存在过点
,则是否存在过点![]() 且不与
且不与![]() 轴重合的直线
轴重合的直线![]() (记直线
(记直线![]() 与椭圆
与椭圆![]() 的交点为
的交点为![]() ),使得点
),使得点![]() 在以线段
在以线段![]() 为直径的圆上;若存在,求出直线
为直径的圆上;若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=Asin(ωx+φ)(A≠0,ω>0,![]() <φ<
<φ<![]() )的图象关于直线
)的图象关于直线![]() 对称,它的最小正周期为π,则( )
对称,它的最小正周期为π,则( )
A. f(x)的图象过点(0,![]() ) B. f(x)在
) B. f(x)在![]() 上是减函数
上是减函数
C. f(x)的一个对称中心是![]() D. f(x)的一个对称中心是
D. f(x)的一个对称中心是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
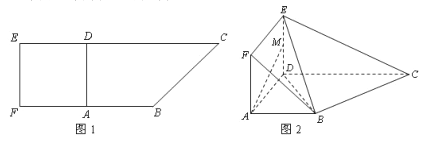
【题目】如图 1,在直角梯形![]() 中,
中, ![]() ,且
,且![]() .现以
.现以![]() 为一边向形外作正方形
为一边向形外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使
翻折,使![]() 平面与平面
平面与平面![]() 垂直,
垂直, ![]() 为
为![]() 的中点,如图 2.
的中点,如图 2.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M: ![]() 及其上一点A(2,4)
及其上一点A(2,4)

(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,o)满足:存在圆M上的两点P和Q,使得![]() ,求实数t的取值范围。
,求实数t的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com