
给出下列命题:
①半径为2,圆心角的弧度数为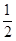 的扇形面积为
的扇形面积为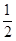 ;
;
②若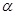 、
、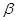 为锐角,
为锐角,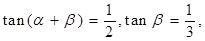 则
则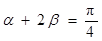 ;
;
③函数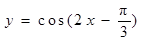 的一条对称轴是
的一条对称轴是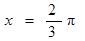 ;
;
④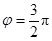 是函数
是函数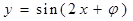 为偶函数的一个充分不必要条件.
为偶函数的一个充分不必要条件.
其中真命题的序号是 .
②③④
【解析】
试题分析:根据题意分别判定
①由扇形的面积公式可得S= ×22=1,则半径为2,圆心角的弧度数为
×22=1,则半径为2,圆心角的弧度数为 的扇形面积为1;故①错误
的扇形面积为1;故①错误
②由α、β为锐角,tan(α+β)= <1,tan β
<1,tan β <1,可得0<α+β<
<1,可得0<α+β< ,0<β<
,0<β< ,∴0<α+2β<
,∴0<α+2β<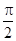 ,则tan(α+2β)=tan[(α+β)+β]=
,则tan(α+2β)=tan[(α+β)+β]=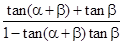 =1
=1
∴α+2β= ;故②正确③当x=
;故②正确③当x= 时,函数y=cos(2x-
时,函数y=cos(2x-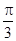 )=cosπ=-1取得函数的最小值,根据函数对称轴处取得最值的性质可知,函数的一条对称轴是x=
)=cosπ=-1取得函数的最小值,根据函数对称轴处取得最值的性质可知,函数的一条对称轴是x= ;③正确
;③正确
④∅=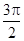 时,函数y=sin(2x+ϕ)=-cos2x为偶函数,但是当y=sin(2x+ϕ)为偶函数时,kπ+
时,函数y=sin(2x+ϕ)=-cos2x为偶函数,但是当y=sin(2x+ϕ)为偶函数时,kπ+ π=∅,即∅=
π=∅,即∅=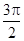 是函数y=sin(2x+ϕ)为偶函数时的一个充分不必要条件.④正确
是函数y=sin(2x+ϕ)为偶函数时的一个充分不必要条件.④正确
故答案为:②③④
考点:本试题主要以命题的真假关系的判断为载体,主要考查了扇形的面积公式、两角和的正切公式、正弦函数与余弦函数的对称性质等知识的综合应用,此类试题综合性强,考查的知识点较多.
点评:解决该试题的关键对于三角函数性质的熟练运用。


科目:高中数学 来源: 题型:
| x2 |
| 4-t |
| y2 |
| t-1 |
| 5 |
| 2 |
| 5-2t |
| 1-t |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源:上海市十校2012届高三第二次联考数学文科试题 题型:022
下图展示了一个区间(0,k)(k是一个给定的正实数)到实数集R的对应过程:区间(0,k)中的实数m对应线段AB上的点M,如图1;将线段AB弯成半圆弧,圆心为H,如图2;再将这个半圆置于直角坐标系中,使得圆心H坐标为(0,1),直径AB平行x轴,如图3;在图形变化过程中,图1中线段AM的长度对应于图3中的圆弧AM的长度,直线HM与直线y=-1相交与点N(n,-1),则与实数m对应的实数就是n,记作n=f(m).给出下列命题:

(1)![]() ;
;
(2)函数n=f(m)是奇函数;
(3)n=f(m)是定义域上的单调递增函数;
(4)n=f(m)的图象关于点![]() 对称;
对称;
(5)方程f(m)=2的解是![]() .
.
其中正确命题序号为________.
查看答案和解析>>
科目:高中数学 来源:上海市十校2012届高三第二次联考数学理科试题 题型:022
下图展示了一个区间(0,k)(k是一个给定的正实数)到实数集R的对应过程:区间(0,k)中的实数m对应线段AB上的点M,如图1;将线段AB弯成半圆弧,圆心为H,如图2;再将这个半圆置于直角坐标系中,使得圆心H坐标为(0,1),直径AB平行x轴,如图3;在图形变化过程中,图1中线段AM的长度对应于图3中的圆弧AM的长度,直线HM与直线y=-1相交与点N(n,-1),则与实数m对应的实数就是n,记作n=f(m).给出下列命题:

(1)![]() ;(2)函数n=f(m)是奇函数;(3)n=f(m)是定义域上的单调递增函数;(4)n=f(m)的图象关于点
;(2)函数n=f(m)是奇函数;(3)n=f(m)是定义域上的单调递增函数;(4)n=f(m)的图象关于点![]() 对称;(5)方程f(m)=2的解是
对称;(5)方程f(m)=2的解是![]() .
.
其中正确命题序号为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com