
【题目】解答题。
(1)求函数f(x)=x2﹣2x+2.在区间[ ![]() ,3]上的最大值和最小值;
,3]上的最大值和最小值;
(2)已知f(x)=ax3+bx﹣4,若f(2)=6,求f(﹣2)的值
(3)计算0.0081 ![]() +(4
+(4 ![]() )2+(
)2+( ![]() )
) ![]() ﹣16﹣0.75+3
﹣16﹣0.75+3 ![]() 的值.
的值.
【答案】
(1)解:f(x)=(x﹣1)2+1,
∴f(x)的对称轴为x=1,
∴f(x)在[ ![]() ,1]上是减函数,在(1,3]上是增函数,
,1]上是减函数,在(1,3]上是增函数,
∴fmax(x)=f(3)=5,fmin(x)=f(1)=1
(2)解:令g(x)=f(x)+4=ax3+bx,
则g(x)是奇函数,
∵f(2)=6,∴g(2)=f(2)+4=10,
∴g(﹣2)=﹣10,即f(﹣2)+4=﹣10,
∴f(﹣2)=﹣14
(3)解:0.0081 ![]() +(4
+(4 ![]() )2+(
)2+( ![]() )
) ![]() ﹣16﹣0.75+3
﹣16﹣0.75+3 ![]()
=(0.34) ![]() +(22)
+(22) ![]() +(2
+(2 ![]() )
) ![]() ﹣(24)
﹣(24) ![]() +4
+4
=0.3+2﹣3+2﹣2﹣2﹣3+4
= ![]() +
+ ![]() +4
+4
= ![]()
【解析】(1)判断f(x)的单调性,根据单调性和对称性得出f(x)的最值;(2)令g(x)=f(x)+4=ax3+bx,利用g(x)的奇偶性求出g(﹣2),从而得出f(﹣2);(3)根据分数指数幂的运算法则计算.
【考点精析】掌握二次函数的性质和对数的运算性质是解答本题的根本,需要知道当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减;①加法:
上递减;①加法:![]() ②减法:
②减法:![]() ③数乘:
③数乘:![]() ④
④![]() ⑤
⑤![]() .
.


科目:高中数学 来源: 题型:
【题目】某中学举行了一次“环保只知识竞赛”,全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为![]() 分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表(如图所示),解决下列问题.
分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表(如图所示),解决下列问题.

(1)求出![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩是![]() 分以上(含
分以上(含![]() 分)的同学中随机抽取
分)的同学中随机抽取![]() 名同学到广场参加环保只是的志愿宣传活动.
名同学到广场参加环保只是的志愿宣传活动.
1)求所抽取的![]() 名同学中至少有
名同学中至少有![]() 名同学来自第
名同学来自第![]() 组的概率;
组的概率;
2)求所抽取的![]() 名同学来自同一组的概率.
名同学来自同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)、g(x)分别是定义在R上的奇函数和偶函数,令h(x)=f(x)g(x),且对任意x1 , x2∈(0,+∞),都有 ![]() <0,g(1)=0,则不等式xh(x)<0的解集为 .
<0,g(1)=0,则不等式xh(x)<0的解集为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.
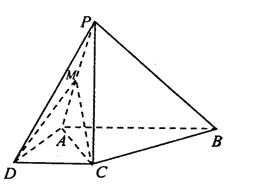
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 为线段
为线段![]() 的中点,且过
的中点,且过![]() 三点的平面与线段
三点的平面与线段![]() 交于点
交于点![]() ,确定点
,确定点![]() 的位置,说明理由;并求三棱锥
的位置,说明理由;并求三棱锥![]() 的高.
的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com