
已知函数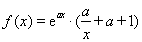 ,其中
,其中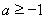 .
.
(Ⅰ)当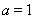 时,求曲线
时,求曲线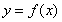 在点
在点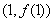 处的切线方程;
处的切线方程;
(Ⅱ)求f(x)的单调区间.
(Ⅰ)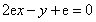 (Ⅱ)① 当
(Ⅱ)① 当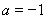 时, 单调递减区间为
时, 单调递减区间为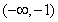 ;单调递增区间为
;单调递增区间为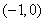 ,
, .②当
.②当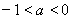 时,
时,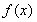 的单调递减区间为
的单调递减区间为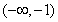 ,
, ;单调递增区间为
;单调递增区间为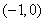 ,
,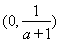 ③ 当
③ 当 时,
时,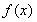 为常值函数,不存在单调区间.④当
为常值函数,不存在单调区间.④当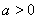 时,
时,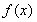 的单调递减区间为
的单调递减区间为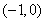 ,
,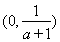 ;单调递增区间为
;单调递增区间为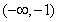 ,
,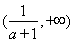 .
.
【解析】(Ⅰ)【解析】
当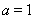 时,
时,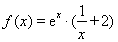 ,
,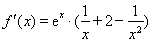 .………………2分
.………………2分
由于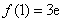 ,
,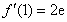 ,
,
所以曲线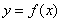 在点
在点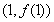 处的切线方程是
处的切线方程是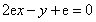 . ………………4分
. ………………4分
(Ⅱ)【解析】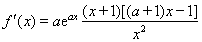 ,
,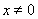 . ………………6分
. ………………6分
① 当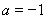 时,令
时,令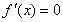 ,解得
,解得 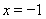 .
.
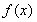 的单调递减区间为
的单调递减区间为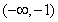 ;单调递增区间为
;单调递增区间为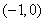 ,
, .……………8分
.……………8分
当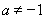 时,令
时,令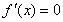 ,解得
,解得 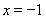 ,或
,或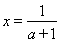 .
.
② 当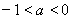 时,
时,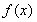 的单调递减区间为
的单调递减区间为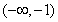 ,
, ;单调递增区间为
;单调递增区间为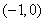 ,
,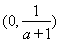 ………………10分
………………10分
③ 当 时,
时,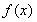 为常值函数,不存在单调区间.………………11分
为常值函数,不存在单调区间.………………11分
④ 当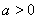 时,
时,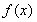 的单调递减区间为
的单调递减区间为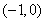 ,
,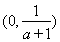 ;单调递增区间为
;单调递增区间为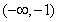 ,
,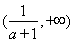 .………………13分
.………………13分


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:解答题
为缓解某路段交通压力,计划将该路段实施“交通限行”.在该路段随机抽查了50人,了解公众对“该路段限行”的态度,将调查情况进行整理,制成下表:
年龄 (岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频 数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成 人数 | 4 | 8 | 9 | 6 | 4 | 3 |
(1)作出被调查人员年龄的频率分布直方图.
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“交通限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十七选修4-4第一节练习卷(解析版) 题型:解答题
在极坐标系(ρ,θ)(0≤θ<2π)中,求曲线ρ=2sinθ与ρcosθ=1的交点Q的极坐标.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:选择题
在15个村庄中有7个村庄交通不方便,现从中任意选10个村庄,用X表示这10个村庄中交通不方便的村庄数,下列概率中等于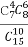 的是( )
的是( )
(A)P(X=2) (B)P(X≤2)
(C)P(X=4) (D)P(X≤4)
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数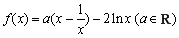 .
.
(Ⅰ)若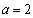 ,求曲线
,求曲线 在点
在点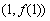 处的切线方程;
处的切线方程;
(Ⅱ)求函数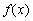 的单调区间;
的单调区间;
(Ⅲ)设函数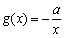 .若至少存在一个
.若至少存在一个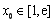 ,使得
,使得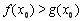 成立,求实数
成立,求实数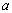 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数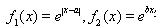
(I)若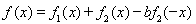 ,是否存在a,b
,是否存在a,b R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
〔II)若a=2,b=1.求函数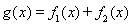 在R上的单调区间;
在R上的单调区间;
(III )对于给定的实数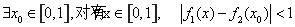 成立.求a的取值范围.
成立.求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:解答题
本着健康、低碳的生活理念,租自行车骑游的人越来越多。某自行车租车点的收费标准是每车每次租车时间不超过两小时免费,超过两小时的部分每小时收费标准为2元(不足1小时的部分按1小时计算)。有甲乙两人相互独立来该租车点租车骑游(各租一车一次),设甲、乙不超过两小时还车的概率分别为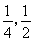 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为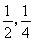 ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(1)求出甲、乙两人所付租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量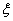 ,求
,求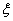 的分布列与数学期望
的分布列与数学期望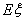 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com