
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.
现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min,在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1 260 m,经测量,cos A=![]() ,cos C=
,cos C=![]() .
.
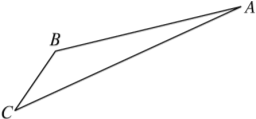
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
【答案】(1)1 040 m;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)在![]() 中,因为cos A=
中,因为cos A=![]() ,cos C=
,cos C=![]() ,所以sin A=
,所以sin A=![]() ,sin C=
,sin C=![]() .
.
从而sin B=sin[π-(A+C)]=sin(A+C)=sin Acos C+cos Asin C=![]() .
.
由正弦定理![]() ,可得
,可得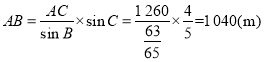 .
.
所以索道AB的长为1 040 m.(3分)
(2)假设乙出发t 分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t m,
所以由余弦定理,得![]() ,
,
因为![]() ,即0≤t≤8,所以当
,即0≤t≤8,所以当![]() 分钟时,甲、乙两游客距离最短.(6分)
分钟时,甲、乙两游客距离最短.(6分)
(3)由正弦定理![]() ,得
,得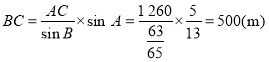 .
.
乙从B出发时,甲已走了50×(2+8+1)=550(m),还需走710 m才能到达C.
设乙步行的速度为v m/min,由题意得![]() ,解得
,解得![]() ,
,
所以为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在![]() (单位:m/min)范围内.(10分)
(单位:m/min)范围内.(10分)


科目:高中数学 来源: 题型:
【题目】为了调查高一新生中女生的体重情况,校卫生室随机选20名女生作为样本,测量她们的体重(单位:kg),获得的所有数据按照区间![]() ,
, ![]() ,
, ![]() ,
, ![]() 进行分组,得到频率分布直方图如图所示,已知样本中体重在区间
进行分组,得到频率分布直方图如图所示,已知样本中体重在区间![]() 上的女生数与体重在区间
上的女生数与体重在区间![]() 上的女生数之比为
上的女生数之比为![]() .
.

(1)求![]() 的值;
的值;
(2)从样本中体重在区间![]() 上的女生中随机抽取两人,求体重在区间
上的女生中随机抽取两人,求体重在区间![]() 上的女生至少有一人被抽中的概率.
上的女生至少有一人被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知袋中放有形状大小相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球![]() 个,从袋中随机抽取一个小球,取到标号为2的小球的概率为
个,从袋中随机抽取一个小球,取到标号为2的小球的概率为![]() ,现从袋中不放回地随机取出2个小球,记第一次取出的小球标号为
,现从袋中不放回地随机取出2个小球,记第一次取出的小球标号为![]() ,第二次取出的小球标号为
,第二次取出的小球标号为![]() .
.
(1)记“![]() ”为事件
”为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
(2)在区间![]() 上任取两个实数
上任取两个实数![]() ,求事件
,求事件![]() “
“![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“鸡兔同笼”问题是我国古代著名的趣题之一.《孙子算经》中就记载了这个有趣的问题.书中这样描述:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔几何?
试设计一个算法,输入鸡兔的总数量和鸡兔的脚的总数量,分别输出鸡、兔的数量,写出程序语句.并画出相应的程序框图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 上每一点的纵坐标不变,横坐标变为原来的
上每一点的纵坐标不变,横坐标变为原来的![]() ,得曲线C.
,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线l: ![]() 与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程.
与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
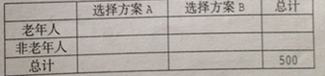
【题目】为丰富人民群众业余生活,某市拟建设一座江滨公园,通过专家评审筛选处建设方案A和B向社会公开征集意见,有关部分用简单随机抽样方法调查了500名市民对这两种方案的看法,结果用条形图表示如下:
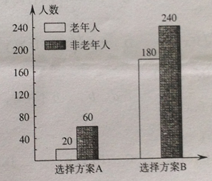
(1)根据已知条件完成下面![]() 列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过
列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过![]() 的前提下认为是否选择方案A和年龄段有关?
的前提下认为是否选择方案A和年龄段有关?
(2)根据(1)的结论,能否提出一个更高的调查方法,使得调查结果更具代表性,说明理由.
附:

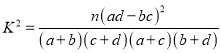
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )将
)将![]() 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数![]() 的图象.
的图象.
(1)求函数![]() 的解析式;
的解析式;
(2)若方程![]() 在
在![]() 上有且仅有一个实根,求
上有且仅有一个实根,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称,设
对称,设![]() ,已知
,已知![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com