
(
北京海淀模拟)如下图,已知平行六面体 的底面为正方形,
的底面为正方形, 、O分别为上、下底面的中心,且
、O分别为上、下底面的中心,且 在底面ABCD上的射影是O.
在底面ABCD上的射影是O.

(1)
求证:平面 ⊥平面ABCD;
⊥平面ABCD;
(2)
若点E,F分别在棱 ,BC上,且
,BC上,且 ,问点F在何处时,EF⊥AD?
,问点F在何处时,EF⊥AD?
(3)
若 ,求二面角C-
,求二面角C- -B的大小(用反三角函数表示).
-B的大小(用反三角函数表示). |
解析: (1)连结AC,BD,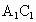 ,则O为AC,BD的交点, ,则O为AC,BD的交点,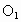 为 为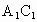 , ,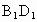 的交点.由平行六面体的性质知: 的交点.由平行六面体的性质知: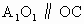 且 且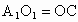 , ,
∴四边形 ∴ 又∵ ∴ 又∵ ∴平面 (2) 作EH⊥平面ABCD,垂足为H,则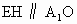 ,点H在直线AC上,且EF在平面ABCD上的射影为HF.由三垂线定理及其逆定理, ,点H在直线AC上,且EF在平面ABCD上的射影为HF.由三垂线定理及其逆定理,
知 ∵ 从而 CH=2AH.又∵HF∥AB,∴ CF=2BF,从而 . .
∴当 F为BC的三等分点(靠近B)时,有EF⊥AD.(2) 过点O作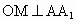 ,垂足为M,连结BM. ,垂足为M,连结BM.
∵ 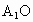 ⊥平面ABCD, ⊥平面ABCD,
∴ 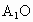 ⊥OB. ⊥OB.
又∵ OB⊥OA.∴OB⊥平面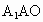 ,由三垂线定理得 ,由三垂线定理得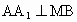 . .
∴∠ OMB为二面角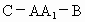 的平面角, 的平面角,
在 Rt△AMB中,∠MAB=60°,∴ 又∵ ∴ ∴二面角 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:022
(2007
北京海淀模拟)某资料室在计算机使用中,如下表所示,编码以一定规律排列,且从左至右以及从上到下都是无限的.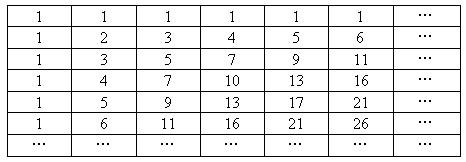
此表中,主对角线上数列
1,2,5,10,17,…的通项公式为________;编码100共出现________次.查看答案和解析>>
科目:高中数学 来源: 题型:044
(
北京海淀模拟)如图所示,有一种“数独”推理游戏,游戏规则如下:
①在
9×9的九宫格子中,分成9个3×3的小九宫格,用1到9这9个数字填满整个格子;②每一行与每一列都有
1到9的数字,每个小九宫格里也有1到9的数字,并且一个数字在每行、每列及每个小九宫格里只能出现一次,既不能重复也不能少.那么A处应填入的数字为________;B处应填入的数字为________.查看答案和解析>>
科目:高中数学 来源: 题型:013
(2007
北京海淀模拟)函数y=kx+b,其中k,b(k≠0)是常数,其图象是一条直线,称这个函数为线性函数,对于非线性可导函数f(x),在点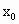 附近一点x的函数值f(x),可以用如下方法求其近似代替值:
附近一点x的函数值f(x),可以用如下方法求其近似代替值: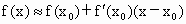 .利用这一方法,
.利用这一方法,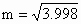 的近似代替值
的近似代替值
[
]|
A .大于m |
B .小于m |
|
C .等于m |
D .与m的大小关系无关 |
查看答案和解析>>
科目:高中数学 来源: 题型:044
(
北京海淀模拟)某选手进行实弹射击训练,射击中每次射击的结果是相互独立的,已知他每次射击时,命中环数ξ的分布如下表:
该选手在训练时先射击三次,若三次射击的总环数不小于
29环,则射击训练停止;若三次射击的总环数小于29环,则再射击三次,然后训练停止.(1)
求该选手在射击训练中恰好射击三次的概率;(2)
求该选手训练停止时,射击的次数η的分布列及期望.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com