练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列推理过程不是演绎推理的是（ ）．

    ①一切奇数都不能被2整除，2019是奇数， 2019不能被2整除；

    ②由“正方形面积为边长的平方”得到结论：正方体的体积为棱长的立方；

    ③在数列中，，，由此归纳出的通项公式；

    ④由“三角形内角和为”得到结论：直角三角形内角和为 .

    A. ① ② B. ② ③ C. ③ ④ D. ②④

    【答案】B

    【解析】分析: 演绎推理的模式是三段论模式，包括大前提，小前提和结论，演绎推理的特点是从一般到特殊，根据上面的特点，判断下面四个结论是否正确，结果③是一个归纳推理，②是一个类比推理，①④是演绎推理．

    详解：演绎推理的模式是三段论模式，包括大前提，小前提和结论，

    演绎推理的特点是从一般到特殊，

    根据上面的特点，判断下面四个结论是否正确，

    ①一切奇数都不能被2整除，2019是奇数， 2019不能被2整除，是演绎推理，故①不选；

    ②由“正方形面积为边长的平方”得到结论：正方体的体积为棱长的立方，是类比推理，

    不是演绎推理，故选②；

    ③在数列中，，，由此归纳出的通项公式，是归纳推理

    不是演绎推理，故选③；

    ④由“三角形内角和为”得到结论：直角三角形内角和为，是演绎推理，

    故④不选；

    总上可知②③符合要求，

    故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，已知四棱锥P﹣ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E，F分别是BC，PC的中点． （I）证明：AE⊥PD；
    （II）H是PD上的动点，EH与平面PAD所成的最大角为45°，求二面角E﹣AF﹣C的正切值．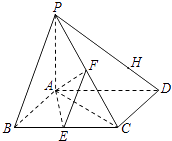

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，f（x）=|x﹣a|
    （Ⅰ）当a=2，解不等式，f（x）≥5﹣|x﹣1|；
    （Ⅱ）若f（x）≤1的解集为[0，2]，+=a（m＞0，n＞0），求证：m+2n≥4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，是偶函数．

    （1）求的值；

    （2）若函数的图象在直线上方，求的取值范围；

    （3）若函数，，是否存在实数使得的最小值为0？若存在，求出的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列关于回归分析的说法中错误的有（ ）个

    (1). 残差图中残差点所在的水平带状区域越宽，则回归方程的预报精确度越高.

    (2). 回归直线一定过样本中心。

    (3). 两个模型中残差平方和越小的模型拟合的效果越好。

    (4) .甲、乙两个模型的分别约为0.88和0.80，则模型乙的拟合效果更好.

    A. 4 B. 3 C. 2 D. 1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列类比推理命题(其中为有理数集，为实数集，为复数集)，其中类比结论正确的是（ ）

    A. “若，则”类比推出“若，则”.

    B. 类比推出

    C. 类比推出

    D. “若，则”类比推出“若，则”.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是定义在上的奇函数，且，当a，，时，有成立．

    Ⅰ求在区间1上的最大值；

    Ⅱ若对任意的都有，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对任意等比数列{an}，下列说法一定正确的是（ ）
    A.a1 ， a3 ， a9成等比数列
    B.a2 ， a3 ， a6成等比数列
    C.a2 ， a4 ， a8成等比数列
    D.a3 ， a6 ， a9成等比数列

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】第一届“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行，这是2017年我国重要的主场外交活动，对推动国际和地区合作具有重要意义．某高中政教处为了调查学生对“一带一路”的关注情况，在全校组织了“一带一路知多少”的知识问卷测试，并从中随机抽取了12份问卷，得到其测试成绩（百分制），如茎叶图所示．

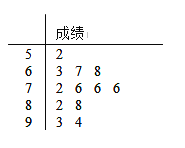
    （1）写出该样本的众数、中位数，若该校共有3000名学生，试估计该校测试成绩在70分以上的人数；

    （2）从所抽取的70分以上的学生中再随机选取4人．

    ①记表示选取4人的成绩的平均数，求；

    ②记表示测试成绩在80分以上的人数，求的分布和数学期望．

    查看答案和解析>>

    同步练习册答案