
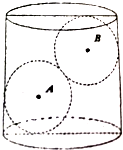
 如图,在水平放置的直径与高相等的圆柱内,放入两个半径相等的小球(球A和球B),圆柱的底面直径为2+$\sqrt{2}$,向圆柱内注满水,水面刚好淹没小球B
如图,在水平放置的直径与高相等的圆柱内,放入两个半径相等的小球(球A和球B),圆柱的底面直径为2+$\sqrt{2}$,向圆柱内注满水,水面刚好淹没小球B分析 (Ⅰ)设圆柱的半径为R,小球的半径为r,且r<R,利用勾股定理可求出r的值,进而得到球A的体积;
(Ⅱ)分别求出球的表面积和圆柱的侧面积,可得答案.
解答 解:(Ⅰ)设圆柱的半径为R,小球的半径为r,且r<R
由圆柱与球的性质知AB2=(2r)2=(2R-2r)2+(2R-2r)2,
即r2-4Rr+2R2=0,
∵r<R,
∴$r=(2-\sqrt{2})R=(2-\sqrt{2})\frac{{2+\sqrt{2}}}{2}=1$
∴球A的体积$V=\frac{4}{3}π{r^3}=\frac{4}{3}π$…(6分)
(Ⅱ)球B的表面积${S_{球B}}=4π{r^2}=4πr$
圆柱的侧面积${S_{圆柱}}=2πR•2R=4π{R^2}=(6+4\sqrt{2})π$
∴圆柱的侧面积与球B的表面积之比为$\frac{{3+2\sqrt{2}}}{2}$. …(6分)
点评 本题考查的知识点是旋转体,球的体积与表面积公式,圆柱的侧面积公式,其中求出球的半径r是解答的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在△ABC中,a:b:c=sinA:sinB:sinC | |
| B. | 在△ABC中,a=b⇒sin2A=sin2B | |
| C. | 在△ABC中,余弦值较小的角所对的边也较小 | |
| D. | 在△ABC中,$\frac{a}{sinA}=\frac{a+b-c}{sinB-sinC+sinA}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com