练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (1)用二项式定理证明1110－1能被100整除．

    (2)求9192被100除所得的余数．

    答案：
    解析：

    　　(1)证明：∵1110－1＝(10＋1)10－1＝(1010＋·109＋…＋·10＋1)－1

    　　＝1010＋·109＋·108＋…＋102

    　　＝100(108＋·107＋·106＋…＋1)．

    　　∴1110－1能被100整除．

    　　(2)解法一：(100－9)92＝·10092－·10091·9＋·10090·92－…＋992，

    　　展开式中前92项均能被100整除，只需求最后一项除以100的余数．

    　　∵992＝(10－1)92＝·1092－·1091＋…＋·102－·10＋1，

    　　前91项均能被100整除，后两项和为－919，因余数为正，可从前面的数中分离出1 000，结果为1 000－919＝81，

    　　故9192被100除可得余数为81．

    　　解法二：(90＋1)92＝·9092＋·9091＋…＋·902＋·90＋．

    　　前91项均能被100整除，剩下两项和为92×90＋1＝8 281，显然8 281除以100所得余数为81．

    　　思路分析：解决利用二项式定理证明整除问题关键是判断所证式子与除数之间的联系，要掌握好对式子的拆分，如本例的第(1)小题，可以利用1110＝(10＋1)10展开式进行证明，第(2)小题则可利用9192＝(100－9)92展开式，或利用(90＋1)92展开式进行求解．


    提示：

    利用二项式定理可以求余数和整除性问题，通常需将底数化成两数的和与差的形式，且这种转化形式与除数有密切的关系．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （1）化简[(a-
    3
    2
    b2)-1(ab-3)
    1
    2
    (b
    1
    2
    )7]
    1
    3
    ．
    （2）解
    1
    6
    lgx=
    1
    3
    lga+2lgb+lgc．
    （3）用二项式定理计算（3.02）4，使误差小于千分之一．
    （4）试证直角三角形弦上的半圆的面积，等于勾上半圆的面积与股上半圆的面积的总和．
    （5）已知球的半径等于r，试求内接正方形的体积．
    （6）已知a是三角形的一边，β及γ是这边的两邻角，试求另一边b的计算公式．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （1）化简[(a-
    3
    2
    b2)-1(ab-3)
    1
    2
    (b
    1
    2
    )7]
    1
    3
    ．
    （2）解
    1
    6
    lgx=
    1
    3
    lga+2lgb+lgc．
    （3）用二项式定理计算（3.02）4，使误差小于千分之一．
    （4）试证直角三角形弦上的半圆的面积，等于勾上半圆的面积与股上半圆的面积的总和．
    （5）已知球的半径等于r，试求内接正方形的体积．
    （6）已知a是三角形的一边，β及γ是这边的两邻角，试求另一边b的计算公式．

    查看答案和解析>>

    科目：高中数学 来源：1954年全国统一高考数学试卷（解析版） 题型：解答题

    （1）化简．
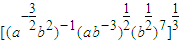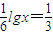    （2）解lga+2lgb+lgc．
    （3）用二项式定理计算（3.02）4，使误差小于千分之一．
    （4）试证直角三角形弦上的半圆的面积，等于勾上半圆的面积与股上半圆的面积的总和．
    （5）已知球的半径等于r，试求内接正方形的体积．
    （6）已知a是三角形的一边，β及γ是这边的两邻角，试求另一边b的计算公式．

    查看答案和解析>>

    同步练习册答案