
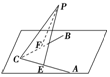
 ∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2$\sqrt{3}$ cm,那么PC与平面ABC所成角的大小为45°.
∠ACB=90°,平面ABC外有一点P,PC=4cm,点P到角的两边AC、BC的距离都等于2$\sqrt{3}$ cm,那么PC与平面ABC所成角的大小为45°. 分析 设P点在ABC平面投影点为O,过P点作BC边的垂线垂足为D,连接OP,OC,OD,根据,∠ACB=90°,平面ABC外一点P满足PC=4,P到两边AC,BC的距离都是2$\sqrt{3}$ cm,我们分别求出CD,OD,OP的长,进而解出∠PCO的大小,即可得到PC与平面ABC所成角的大小.
解答 解:设P点在ABC平面投影点为O,过P点作BC边的垂线垂足为D,
连接OP,OC,OD,如图所示: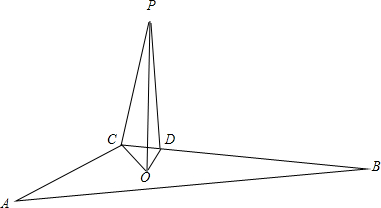
则∠PCO即为PC与平面ABC所成角的平面角
∵P到两边AC,BC的距离都是2$\sqrt{3}$cm,
故O点在∠ACB的角平分线上,即∠OCD=45°
由于PC为4cm,PD为2$\sqrt{3}$cm,则CD为2cm.
则△PCD在底面上的投影△OCD为等腰直角三角形.
则OD=CD=2,然后得CO=2$\sqrt{2}$cm,
根据勾股定理得PO=2$\sqrt{2}$cm=CO,
∴∠PCO=45°.
故答案为:45°.
点评 本题考查的知识点是直线与平面所成的角,其中P点在ABC平面投影点为O,构造出∠PCO即为PC与平面ABC所成角的平面角,将线面夹角问题转化为解三角形问题是解答本题的关键.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则ac2>bc2 | B. | 若a>b>0,则a2>b2 | ||
| C. | 若a>b,c<d,则 a-c<b-d | D. | 若a<b<0,则$\frac{1}{a}<\frac{1}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①②③ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com