
 ?证明你的结论.
?证明你的结论.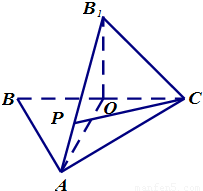
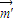 =(0,1,0),
=(0,1,0),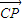 的坐标,根据CP与平面B1OA所成的角的正弦值为
的坐标,根据CP与平面B1OA所成的角的正弦值为 ,利用向量的夹角公式,可得结论.
,利用向量的夹角公式,可得结论.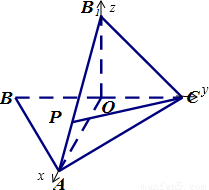 解:(Ⅰ)依题意得OA、OC、OB1两两垂直,分别以射线OA、OC、OB1为x、y、轴的正半轴建立空间直角坐标系O-xyz,
解:(Ⅰ)依题意得OA、OC、OB1两两垂直,分别以射线OA、OC、OB1为x、y、轴的正半轴建立空间直角坐标系O-xyz,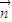 ,可得
,可得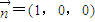
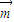 =(x,y,z),
=(x,y,z),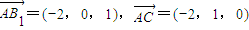
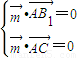 ,可得
,可得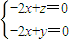 ,∴可取
,∴可取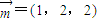
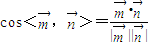 =
=
 ;
;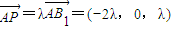 ,则
,则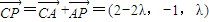
 =(0,1,0),CP与平面B1OA所成的角的正弦值为
=(0,1,0),CP与平面B1OA所成的角的正弦值为
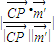 =
=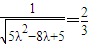
 或λ=
或λ= (舍去)
(舍去)

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
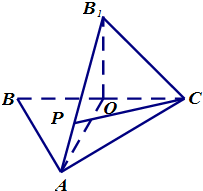 (2012•贵州模拟)如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将三角形BAO沿AO折起,使B点与图中B1点重合,其中B1O⊥平面AOC.
(2012•贵州模拟)如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将三角形BAO沿AO折起,使B点与图中B1点重合,其中B1O⊥平面AOC.| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
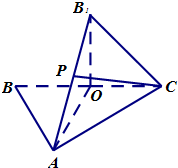 (2012•贵州模拟)如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将三角形BAO沿AO折起,使B点与图中B1点重合,其中B1O⊥平面AOC.
(2012•贵州模拟)如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将三角形BAO沿AO折起,使B点与图中B1点重合,其中B1O⊥平面AOC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
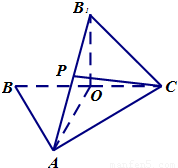
 如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将三角形BAO沿AO折起,使B点与图中B1点重合,其中B1O⊥平面AOC.
如图,△ABC中,O是BC的中点,AB=AC,AO=2OC=2.将三角形BAO沿AO折起,使B点与图中B1点重合,其中B1O⊥平面AOC. ?证明你的结论.
?证明你的结论.查看答案和解析>>
科目:高中数学 来源:2011-2012学年贵州省五校高三第二次联考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com