【题目】2017年11月、12月全国大范围流感爆发，为研究昼夜温差大小与患感冒人数多少之间的关系，一兴趣小组抄录了某医院11月到12月间的连续6个星期的昼夜温差情况与因患感冒而就诊的人数，得到如下资料:
日期 | 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | 第六周 |
昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选取的2组数据进行检验。
(Ⅰ)求选取的2组数据恰好是相邻两个星期的概率；
(Ⅱ)若选取的是第一周与第六周的两组数据，请根据第二周到第五周的4组数据,求出
关于
的线性回归方程
；
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考公式: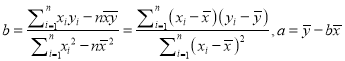 
)
参考数据： 
1092， 
498
【答案】(Ⅰ) 
;(Ⅱ)见解析;(Ⅲ)见解析.
【解析】试题分析：(Ⅰ)用列举法列出所有的基本事件，再找出相邻两个星期的数据的事件个数，利用古典概型的概率公式即可求得；(Ⅱ)根据所给数据分别算出
， 
，再根据求线性回归方程系数的方法求得
，把
， 
和
代入到求
得公式，求出
，即可求出线性回归方程；(Ⅲ)根据所求的线性回归方程，将
和
代入求得
，再同原来表中所给的
和
对应的值做差，差的绝对值不超过
，即可得到线性回归方程理想．
试题解析：(Ⅰ)将连续六组数据分别记为
，从六组中任意选取两组，其基本事件为： 
，共15种情况.
其中两组是相邻的为
，共5种情况.
设抽到相邻两个星期的数据为事件
，则抽到相邻两个星期的数据的概率为
.
(Ⅱ)由数据求得
，由公式求得
，再由
.
∴
关于
的线性回归方程为
(Ⅲ)当
时, 
, 
；
同样, 当
时, 
, 
.
∴该小组所得线性回归方程是理想的
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案科目：高中数学 来源： 题型：
【题目】某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿市场销售价与上市时间的关系用图（1）的一条折线表示；西红柿的种植成本与上市时间的关系用图（2）的抛物线段表示.
（1）写出图（1）表示的市场售价与时间的函数关系式
写出图（2）表示的种植成本与时间的函数关系式
（2）认定市场售价减去种植成本为纯收益，问何时上市的西红柿收益最大？（注：市场售价和种植成本的单位：元/
kg，时间单位：天.）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某区的区人大代表有教师6人，分别来自甲、乙、丙、丁四个学校，其中甲校教师记为
，乙校教师记为
，丙校教师记为
，丁校教师记为
.现从这6名教师代表中选出3名教师组成十九大报告宣讲团，要求甲、乙、丙、丁四个学校中，每校至多选出1名.
（1）请列出十九大报告宣讲团组成人员的全部可能结果；
（2）求教师
被选中的概率；
（3）求宣讲团中没有乙校教师代表的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高二（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，且将全班25人的成绩记为
由右边的程序运行后,输出
.据此解答如下问题：
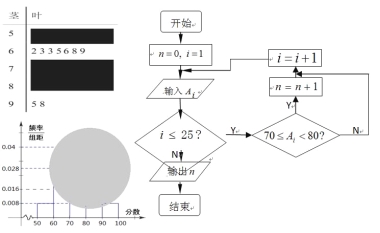
（Ⅰ）求茎叶图中破损处分数在[50，60），[70，80），[80，90）各区间段的频数；
（Ⅱ）利用频率分布直方图估计该班的数学测试成绩的众数，中位数分别是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某城市关系要好的
四个家庭各有两个小孩共8人，准备使用滴滴打车软件，分乘甲、乙两辆汽车出去游玩，每车限坐4人，（乘同一辆车的4名小孩不考虑位置差异）.
（1）共有多少种不同的乘坐方式？
（2）若
户家庭的孪生姐妹需乘同一辆车，则乘坐甲车的4名小孩恰有2名来自于同一个家庭的乘坐方式共有多少种？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
过点
，且离心率为
.过抛物线
上一点
作
的切线
交椭圆
于
，
两点.
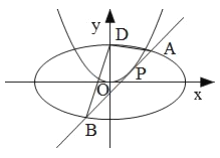
（Ⅰ）求椭圆的方程；
（Ⅱ）是否存在直线，使得
，若存在，求出的方程；若不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
