
【题目】在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:
1 | 2 | 3 | 4 | 5 | |
价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知![]() ,
,
(1)画出散点图;
(2)求出y对x的线性回归方程;
(3)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t).
参考公式: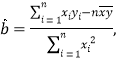
![]() .
.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】已知向量![]() =(sin(A-B),2cosA)
=(sin(A-B),2cosA)![]() =(1,cos(
=(1,cos(![]() -B)),且
-B)),且![]()
![]()
![]() =-sin2C,其中A、B、C分别为△ABC的三边a、b、c所对的角.
=-sin2C,其中A、B、C分别为△ABC的三边a、b、c所对的角.
(Ⅰ)求角C的大小;
(Ⅱ)若sinA+sinB=![]() sinC,且
sinC,且![]() , 求c.
, 求c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图.
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两同学5次综合测评的成绩如茎叶图所示.
甲 | 乙 | |||||
9 | 8 | 8 | 3 | 3 | 7 | |
2 | 1 | 0 | 9 | ● | 9 |
老师在计算甲、乙两人平均分时,发现乙同学成绩的一个数字无法看清.若从{0,1,2,…,9}随机取一个数字代替,则乙的平均成绩超过甲的平均成绩的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
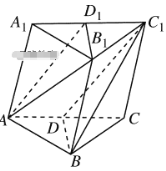
【题目】如图所示,在斜三棱柱ABC—A1B1C1中,点D,D1分别为AC,A1C1上的点.
(1)当![]() 的值等于何值时,BC1∥平面AB1D1;
的值等于何值时,BC1∥平面AB1D1;
(2)若平面BC1D∥平面AB1D1,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2+lnx.
(Ⅰ)当a=﹣1时,求函数y=f(x)的图象在点(1,f(1))处的切线方程;
(Ⅱ)已知a<0,若函数y=f(x)的图象总在直线y=-![]() 的下方,求a的取值范围;
的下方,求a的取值范围;
(Ⅲ)记f′(x)为函数f(x)的导函数.若a=1,试问:在区间[1,10]上是否存在k(k<100)个正数x1 , x2 , x3…xk , 使得f′(x1)+f′(x2)+f′(x3)+…+f′(xk)≥2012成立?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图l,在正方形ABCD中,AB=2,E是AB边的中点,F是BC边上的一点,对角线AC分别交DE、DF于M、N两点.将ADAE,CDCF折起,使A、C重合于A点,构成如图2所示的几何体.
(I)求证:A′D⊥面A′EF;
(Ⅱ)试探究:在图1中,F在什么位置时,能使折起后的几何体中EF∥平面AMN,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对应的边分别为a,b,c.
(1)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(2)若a,b,c成等比数列,求cosB的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() ,
, ![]() ,
, ![]() 是非零向量,已知命题p:若
是非零向量,已知命题p:若 ![]()
![]() =0,
=0, ![]()
![]() =0,则
=0,则 ![]()
![]() =0;命题q:若
=0;命题q:若 ![]() ∥
∥ ![]() ,
, ![]() ∥
∥ ![]() ,则
,则 ![]() ∥
∥ ![]() ,则下列命题中真命题是( )
,则下列命题中真命题是( )
A.p∨q
B.p∧q
C.(¬p)∧(¬q)
D.p∨(¬q)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com