
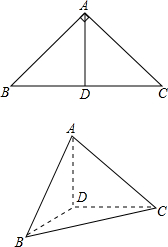
 如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC=90°,若BD=1,求三棱锥D-ABC的表面积.
如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC=90°,若BD=1,求三棱锥D-ABC的表面积. 分析 根据图形特征可得△ADB、△DBC、△ADC是全等的等腰直角三角形,△ABC是等边三角形,利用三角形面积公式可得三棱锥D-ABC的表面积.
解答 解:∵∠BDC=90°,∴DB⊥DC,
∵折起前AD是BC边上的高,
∴当△ABD折起后,AD⊥DC,AD⊥DB,
又DB∩DC=D,
∴AD⊥平面BDC,
∴DA⊥DB,DC⊥DA,
∵DB=DA=DC=1,∴AB=BC=CA=$\sqrt{2}$,
从而S△ADB=S△DBC=S△ADC=$\frac{1}{2}×1×1$=$\frac{1}{2}$,
S△ABC=$\frac{1}{2}×\sqrt{2}×\sqrt{2}sin60°$=$\frac{\sqrt{3}}{2}$
所以三棱锥D-ABC的表面积为:$\frac{1}{2}×3+\frac{\sqrt{3}}{2}$=$\frac{3+\sqrt{3}}{2}$.
点评 解决平面图形翻折问题的关键是看准翻折后没有发生变化的位置关系,抓住翻折后仍然垂直的直线作为条件,从而解决问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,1)∪(9,+∞) | B. | ($\frac{2}{3}$,1) | C. | ($\frac{2}{3}$,3) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
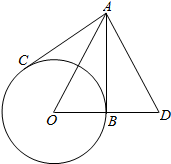 如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )
如图,AB,AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于( )| A. | 70° | B. | 64° | C. | 62° | D. | 51° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
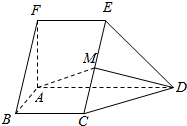 如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.
如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE=$\frac{1}{2}$AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△ABC内接于圆O,AE平分∠BAC交BC于点D,连接BE.
如图,△ABC内接于圆O,AE平分∠BAC交BC于点D,连接BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com