
【题目】下列命题:
①函数![]() 的图象关于
的图象关于![]() 轴对称的充要条件是
轴对称的充要条件是![]() ,
,![]() ;
;
②已知![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,若
项和,若![]() ,则
,则![]() ;
;
③函数![]() 与函数
与函数![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④对于任意两条异面直线,都存在无穷多个平面与这两条异面直线所成的角相等.
其中正确的命题有( )
A.1个B.2个C.3个D.4个
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,建立平面直角坐标系![]() ,
,![]() 轴在地平面上,
轴在地平面上,![]() 轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程
轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程![]() 表示的曲线上,其中
表示的曲线上,其中![]() 与发射方向有关.炮弹的射程是指炮弹落地点的横坐标.
与发射方向有关.炮弹的射程是指炮弹落地点的横坐标.
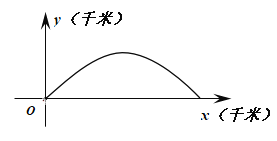
(1)求炮的最大射程;
(2)若规定炮弹的射程不小于6千米,设在此条件下炮弹射出的最大高度为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的一个顶点为![]() ,焦点在x轴上,若右焦点到直线
,焦点在x轴上,若右焦点到直线![]() 的距离为3.
的距离为3.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 设椭圆C与直线
设椭圆C与直线![]() 相交于不同的两点M,N,线段MN的中点为E.
相交于不同的两点M,N,线段MN的中点为E.
![]() 当
当![]() 时,射线OE交直线
时,射线OE交直线![]() 于点
于点![]() 为坐标原点
为坐标原点![]() ,求
,求![]() 的最小值;
的最小值;
![]() 当
当![]() ,且
,且![]() 时,求m的取值范围.
时,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,某企业每年消耗电费约24万元,为了节能减排,决定安装一个可使用15年的太阳能供电设备接入本企业电网,安装这种供电设备的工本费(单位:万元)与太阳能电池板的面积(单位:平方米)成正比,比例系数约为0.5.为了保证正常用电,安装后采用太阳能和电能互补供电的模式.假设在此模式下,安装后该企业每年消耗的电费![]() (单位:万元)与安装的这种太阳能电池板的面积
(单位:万元)与安装的这种太阳能电池板的面积![]() (单位:平方米)之间的函数关系是
(单位:平方米)之间的函数关系是![]() 为常数).记
为常数).记![]() 为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
(1)试解释![]() 的实际意义,并建立
的实际意义,并建立![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 为多少平方米时,
为多少平方米时,![]() 取得最小值?最小值是多少万元?
取得最小值?最小值是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学随机抽取部分高一学生调査其每日自主安排学习的时间(单位:分钟),并将所得数据绘制成如图所示的频率分布直方图,其中自主安排学习时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
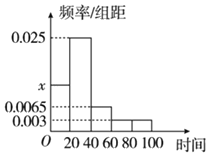
(1)求直方图中x的值;
(2)现采用分层抽样的方式从每日自主安排学习时间不超过40分钟的学生中随机抽取6人,若从这6人中随机抽取2人进行详细的每日时间安排调查,求抽到的2人每日自主安排学习时间均不低于20分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为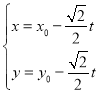 (t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为![]() .
.
(1)求圆C的直角坐标方程及直线![]() 的斜率;
的斜率;
(2)直线![]() 与圆C交于M,N两点,
与圆C交于M,N两点,![]() 中点为Q,求Q点轨迹的直角坐标方程.
中点为Q,求Q点轨迹的直角坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com