
【题目】已知函数f(x)=![]() x2+alnx.
x2+alnx.
(1)若a=﹣1,求函数f(x)的极值,并指出极大值还是极小值;
(2)若a=1,求函数f(x)在[1,e]上的最值;
(3)若a=1,求证:在区间[1,+∞)上,函数f(x)的图象在g(x)=![]() x3的图象下方.
x3的图象下方.
【答案】(1)极小值f(1)=![]() ;(2)
;(2)![]() e2+1;(3)证明见解析
e2+1;(3)证明见解析
【解析】
试题分析:(1)代入a=﹣1,从而化简f(x)并求其定义域,再求导判断函数的单调性及极值即可;
(2)代入a=1,从而化简f(x)并求其定义域,再求导判断函数的单调性及求函数的最值;
(3)代入a=1,令F(x)=g(x)﹣f(x)=![]() x3﹣
x3﹣![]() x2﹣lnx,从而化在区间[1,+∞)上,函数f(x)的图象在g(x)=
x2﹣lnx,从而化在区间[1,+∞)上,函数f(x)的图象在g(x)=![]() x3的图象下方为F(x)>0在[1,+∞)上恒成立,再化为函数的最值问题即可.
x3的图象下方为F(x)>0在[1,+∞)上恒成立,再化为函数的最值问题即可.
解:(1)当a=﹣1时,f(x)=![]() x2﹣lnx的定义域为(0,+∞),
x2﹣lnx的定义域为(0,+∞),
f′(x)=x﹣![]() =
=![]() ;
;
故f(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
故f(x)在x=1处取得极小值f(1)=![]() ;
;
(2)当a=1时,f(x)=![]() x2+lnx的定义域为(0,+∞),
x2+lnx的定义域为(0,+∞),
f′(x)=x+![]() >0;
>0;
故f(x)在[1,e]上是增函数,
故fmin(x)=f(1)=![]() ,fmax(x)=f(e)=
,fmax(x)=f(e)=![]() e2+1;
e2+1;
(3)证明:令F(x)=g(x)﹣f(x)=![]() x3﹣
x3﹣![]() x2﹣lnx;
x2﹣lnx;
则F′(x)=2x2﹣x﹣![]() =
=![]() ,
,
∵x∈[1,+∞),
∴F′(x)=![]() ≥0,
≥0,
∴F(x)在[1,+∞)上是增函数,
故F(x)≥F(1)=![]() ﹣
﹣![]() =
=![]() >0;
>0;
故在区间[1,+∞)上,函数f(x)的图象在g(x)=![]() x3的图象下方.
x3的图象下方.


科目:高中数学 来源: 题型:
【题目】已知直线![]() 过点
过点![]() ,圆
,圆![]() :
:![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(![]() ) 求直线
) 求直线![]() 的方程;
的方程;
(![]() )求直线
)求直线![]() 的斜率
的斜率![]() 的取值范围;
的取值范围;
(Ⅲ)是否存在过点![]() 且垂直平分弦
且垂直平分弦![]() 的直线
的直线![]() ?若存在,求直线
?若存在,求直线![]() 斜率
斜率![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
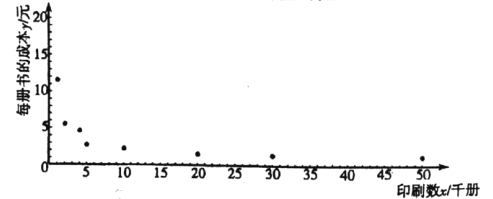
【题目】为研究某种图书每册的成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.
(千册)的关系,收集了一些数据并作了初步处理,得到了下面的散点图及一些统计量的值.

表中![]() ,
, ![]() .
.
(1)根据散点图判断: ![]() 与
与![]() 哪一个更适宜作为每册成本费
哪一个更适宜作为每册成本费![]() (元)与印刷数
(元)与印刷数![]() (千册)的回归方程类型?(只要求给出判断,不必说明理由)
(千册)的回归方程类型?(只要求给出判断,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程(回归系数的结果精确到0.01);
的回归方程(回归系数的结果精确到0.01);
(3)若每册书定价为10元,则至少应该印刷多少千册才能使销售利润不低于78840元?(假设能够全部售出,结果精确到1)
(附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为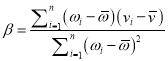 ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一工厂生产了某种产品700件,该工厂对这些产品进行了安全和环保这两个性能的质量检测。工厂决定利用随机数表法从中抽取100件产品进行抽样检测,现将700件产品按001,002,…,700进行编号;
(1)如果从第8行第4列的数开始向右读,请你依次写出最先检测的3件产品的编号;
(下面摘取了随机数表的第7~9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)抽取的100件产品的安全性能和环保性能的质量检测结果如下表:
检测结果分为优等、合格、不合格三个等级,横向和纵向分别表示安全性能和环保性能。若在该样本中,产品环保性能是优等的概率为![]() ,求
,求![]() ,
,![]() 的值。
的值。
件数 | 环保性能 | |||
优等 | 合格 | 不合格 | ||
安全性能 | 优等 | 6 | 20 | 5 |
合格 | 10 | 18 | 6 | |
不合格 |
| 4 |
| |
(3)已知![]() ,
,![]() ,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率。
,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校6个学生的数学和物理成绩如下表:
学生的编号 | 1 | 2 | 3 | 4 | 5 | 6 |
数学 | 89 | 87 | 79 | 81 | 78 | 90 |
物理 | 79 | 75 | 77 | 73 | 72 | 74 |
(1)若在本次考试中,规定数学在80分以上(包括80分)且物理在75分以上(包括75分)的学生为理科小能手.从这6个学生中抽出2个学生,设![]() 表示理科小能手的人数,求
表示理科小能手的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系,在上述表格是正确的前提下,用![]() 表示数学成绩,用
表示数学成绩,用![]() 表示物理成绩,求
表示物理成绩,求![]() 与
与![]() 的回归方程.
的回归方程.
参考数据和公式:![]() ,其中
,其中 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数.
为奇函数.
(1)求a的值,并证明![]() 是R上的增函数;
是R上的增函数;
(2)若关于t的不等式f(t2-2t)+f(2t2-k)<0的解集非空,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com