【题目】设
、
是双曲线
：
的两个焦点，
是上一点，若
，
是△
的最小内角，且
，则双曲线的渐近线方程是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
设|PF1|＞|PF2|，由已知条件求出|PF1|＝4a，|PF2|＝2a，e
，进而求出b
，由此能求出双曲线C：
1的渐近线方程．
设|PF1|＞|PF2|，则|PF1|﹣|PF2|＝2a，
又|PF1|+|PF2|＝6a，解得|PF1|＝4a，|PF2|＝2a．
则∠PF1F2是△PF1F2的最小内角为30°，
∴| PF2|2＝| PF1||2+|F1F2|2﹣2| PF1|||F1F2|cos30°，
∴（2a）2＝（4a）2+（2c）2﹣2×4a×2c
，
同时除以a2，化简e2﹣2
e+3＝0，
解得e，∴c
，∴b
，
∴双曲线C：1的渐近线方程为y
±
，
即
0．
故选：B．
全优点练单元计划系列答案科目：高中数学 来源： 题型：
【题目】已知双曲线
:
的左、右焦点分别为
、
，
为坐标原点，
是双曲线在第一象限上的点，直线
交双曲线左支于点
，直线
交双曲线右支于点
，若
，且
，则双曲线的渐近线方程为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，直线
的倾斜角为
，且经过点
．以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，直线
，从原点O作射线交
于点M，点N为射线OM上的点，满足
，记点N的轨迹为曲线C．
（Ⅰ）求出直线的参数方程和曲线C的直角坐标方程；
（Ⅱ）设直线与曲线C交于P，Q两点，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，AB是圆柱
的一条母线，已知BC过底面圆的圆心O，D是圆O上不与点B、C重合的任意一点，
：
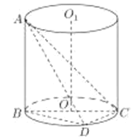
（1）求直线AC与平面ABD所成角的大小；
（2）求点B到平面ACD的距离；
（3）将四面体ABCD绕母线AB旋转一周，求由
旋转而成的封闭几何体的体积；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分14分）如图，在边长为
的菱形
中，
，点
，
分别是边
，
的中点，
．沿
将△
翻折到△
，连接
，得到如图的五棱锥
，且
．
（1）求证：
平面
；
（2）求四棱锥
的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高速公路隧道设计为单向三车道，每条车道宽4米，要求通行车辆限高5米，隧道全长1.5千米，隧道的断面轮廓线近似地看成半个椭圆形状（如图所示）.
（1）若最大拱高
为6米，则隧道设计的拱宽
至少是多少米？（结果取整数）
（2）如何设计拱高和拱宽，才能使半个椭圆形隧道的土方工程量最小？（结果取整数）
参考数据：
，椭圆的面积公式为
，其中
，
分别为椭圆的长半轴和短半轴长.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在边长为8的菱形
中，
，将
沿
折起，使点
到达
的位置，且二面角
为
.
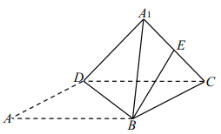
（1）求异面直线
与所成角的大小；
（2）若点
为中点，求直线
与平面
所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线E：
焦点F，过点F且斜率为2的直线与抛物线交于A、B两点，且
．
(1)求抛物线E的方程；
(2)设O是坐标原点，P，Q是抛物线E上分别位于x轴两侧的两个动点，且
①证明：直线PQ必过定点，并求出定点G的坐标；
②过G作PQ的垂线交抛物线于C，D两点，求四边形PCQD面积的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】[选修4—5：参数方程选讲]
在直角坐标系xoy中，曲线
的参数方程是
（t是参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线
的极坐标方程是
(1)求曲线的普通方程和曲线的直角坐标方程；
(2)若两曲线交点为A、B，求
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com