
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,过点
的焦点,过点![]() 任作两条互相垂直的直线
任作两条互相垂直的直线![]() ,
,![]() ,分别交抛物线
,分别交抛物线![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() 四点,
四点,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
(1)求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(2)设直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,试求
两点,试求![]() 的最小值.
的最小值.
【答案】(1)证明见解析,直线![]() 过定点
过定点![]() (2)
(2)![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)设![]() ,
,![]() ,显然直线
,显然直线![]() ,
,![]() 的斜率是存在的,设直线
的斜率是存在的,设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 可得
可得![]() ,可得出
,可得出![]() 的中点坐标为
的中点坐标为![]() ,再根据
,再根据![]() ,得
,得![]() 的中点坐标为
的中点坐标为![]() ,再令
,再令![]() 得
得![]() ,
,
得出直线![]() 恒过点
恒过点![]() ,验证
,验证![]() ,得
,得![]() ,
,![]() ,
,![]() 三点共线,从而直线
三点共线,从而直线![]() 过的定点;
过的定点;
(2))由(1)设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 可得
可得![]() ,再设
,再设 ,
,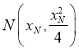 ,得韦达定理
,得韦达定理![]() ,
,![]() ,表示出
,表示出![]() ,由二次函数得出线段
,由二次函数得出线段![]() 的最小值.
的最小值.
(1)设![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 可得
可得![]() ,
,
则![]() ,故
,故![]() ,
,
故![]() 的中点坐标为
的中点坐标为![]() .
.
由![]() ,得
,得![]() ,所以
,所以![]() 的中点坐标为
的中点坐标为![]() .
.
令![]() 得
得![]() ,
,
此时![]() ,故直线
,故直线![]() 过点
过点![]() ,
,
当时![]() ,
,![]() ,
,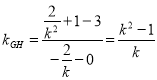 .
.
所以![]() ,
,![]() ,
,![]() ,
,![]() 三点共线,
三点共线,
所以直线![]() 过定点
过定点![]() .
.
(2)设 ,
,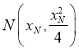 ,直线
,直线![]() 的方程为
的方程为![]() ,
,
代入![]() 可得
可得![]() ,则
,则![]() ,
,![]() ,
,
故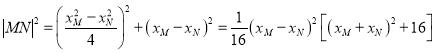
![]()
![]() (当
(当![]() 时,取等号).
时,取等号).
故![]() ,当
,当![]() 及直线
及直线![]() 垂直
垂直![]() 轴时,
轴时,![]() 取得最小值
取得最小值![]() .
.


科目:高中数学 来源: 题型:
【题目】已知平面上两定点M(0,﹣2)、N(0,2),P为一动点,满足![]()
![]() |
|![]() ||
||![]() |
|
(I)求动点P的轨迹C的方程;
(II)若A、B是轨迹C上的两不同动点,且![]() λ
λ![]() .分别以A、B为切点作轨迹C的切线,设其交点Q,证明
.分别以A、B为切点作轨迹C的切线,设其交点Q,证明![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
甲、乙、丙三名射击运动员射中目标的概率分别为![]()
![]() ,三人各射击一次,击中目标的次数记为
,三人各射击一次,击中目标的次数记为![]() .
.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)在概率![]() (
(![]() =0,1,2,3)中, 若
=0,1,2,3)中, 若![]() 的值最大, 求实数
的值最大, 求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,且
,且![]() 为
为![]() 的中点,延长
的中点,延长![]() 交
交![]() 于点
于点![]() ,且
,且![]() 在底
在底![]() 内的射影恰为
内的射影恰为![]() 的中点
的中点![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上任意一点.
上任意一点.
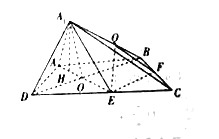
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐角二面角的余弦值.
所成锐角二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有1000名员工,其中男性员工400名,采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查,将计划在今年购买5G手机的员工称为“追光族",计划在明年及明年以后才购买5G手机的员工称为“观望者”,调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人.
(1)完成下列![]() 列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
属于“追光族" | 属于“观望者" | 合计 | |
女性员工 | |||
男性员工 | |||
合计 | 100 |
(2)已知被抽取的这100名员工中有10名是人事部的员工,这10名中有3名属于“追光族”.现从这10名中随机抽取3名,记被抽取的3名中属于“追光族”的人数为随机变量X,求![]() 的分布列及数学期望.
的分布列及数学期望.
附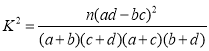 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | p>0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知
中,已知![]() 是曲线
是曲线![]() :
:![]() 上的动点,将
上的动点,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,点![]() ,射线
,射线![]() 与曲线
与曲线![]() ,
,![]() 分别相交于异于极点
分别相交于异于极点![]() 的
的![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且△PF1F2的面积为2.
,且△PF1F2的面积为2.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为1的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于A,B两点,与椭圆C交于C,D两点,且
的圆交于A,B两点,与椭圆C交于C,D两点,且![]() (
(![]() ),当
),当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com