
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上,![]() ,
,![]() ,且
,且![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() ,点
,点![]() 在
在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作
作![]() 的切线
的切线![]() ,若
,若![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设![]() 为坐标原点,动点
为坐标原点,动点![]() 在圆
在圆![]() 上,过
上,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 上的点
上的点![]() 满足
满足![]() .过点
.过点![]() 作直线
作直线![]() 垂直于线段
垂直于线段![]() 交
交![]() 于点
于点![]() .
.
(ⅰ)证明:![]() 恒过定点;
恒过定点;
(ⅱ)设线段![]() 交
交![]() 于点
于点![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】成都七中为了解班级卫生教育系列活动的成效,对全校40个班级进行了一次突击班级卫生量化打分检查(满分100分,最低分20分).根据检查结果:得分在![]() 评定为“优”,奖励3面小红旗;得分在
评定为“优”,奖励3面小红旗;得分在![]() 评定为“良”,奖励2面小红旗;得分在
评定为“良”,奖励2面小红旗;得分在![]() 评定为“中”,奖励1面小红旗;得分在
评定为“中”,奖励1面小红旗;得分在![]() 评定为“差”,不奖励小红旗.已知统计结果的部分频率分布直方图如图:
评定为“差”,不奖励小红旗.已知统计结果的部分频率分布直方图如图:
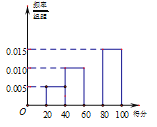
(1)依据统计结果的部分频率分布直方图,求班级卫生量化打分检查得分的中位数;
(2)学校用分层抽样的方法,从评定等级为“良”、“中”的班级中抽取6个班级,再从这6个班级中随机抽取2个班级进行抽样复核,求所抽取的2个班级获得的奖励小红旗面数和不少于3的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为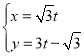 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的参数方程;
的参数方程;
(2)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知M是椭圆C:![]() +
+![]() =1(a>b>0)上一点,F1F2分别为椭圆C的左右焦点,且|F1F2|=2,∠F1MF2=
=1(a>b>0)上一点,F1F2分别为椭圆C的左右焦点,且|F1F2|=2,∠F1MF2=![]() ,△F1MF2的面积为
,△F1MF2的面积为![]() .
.
(1)求椭圆C的方程;
(2)直线l过椭圆C右焦点F2,交该椭圆于AB两点,AB中点为Q,射线OQ交椭圆于P,记△AOQ的面积为S1,△BPQ的面积为S2,若![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下三个条件:
①数列![]() 是首项为 2,满足
是首项为 2,满足![]() 的数列;
的数列;
②数列![]() 是首项为2,满足
是首项为2,满足![]() (λ∈R)的数列;
(λ∈R)的数列;
③数列![]() 是首项为2,满足
是首项为2,满足![]() 的数列..
的数列..
请从这三个条件中任选一个将下面的题目补充完整,并求解.
设数列![]() 的前n项和为
的前n项和为![]() ,
,![]() 与
与![]() 满足______,记数列
满足______,记数列![]() ,
,![]() ,求数列{
,求数列{![]() }的前n项和
}的前n项和![]() ;
;
(注:如选择多个条件分别解答,按第一个解答计分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某央企在一个社区随机采访男性和女性用户各50名,统计他(她)们一天(![]() )使用手机的时间,其中每天使用手机超过6小时(含6小时)的用户称为“手机迷”,否则称其为“非手机迷”,调查结果如下:
)使用手机的时间,其中每天使用手机超过6小时(含6小时)的用户称为“手机迷”,否则称其为“非手机迷”,调查结果如下:
男性用户的频数分布表
男性用户日用时间分组( |
|
|
|
|
|
频数 | 20 | 12 | 8 | 6 | 4 |
女性用户的频数分布表
女性用户日用时间分组( |
|
|
|
|
|
频数 | 25 | 10 | 6 | 8 | 1 |
(1)分别估计男性用户,女性用户“手机迷”的频率;
(2)求男性用户每天使用手机所花时间的中位数;
(3)求女性用户每天使用手机所花时间的平均数与标准差(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com