
分析 由题意把正四面体A-BCD放到正方体BK内,则平面ACD与平面AEF所成角的正弦值等于平面ACD的法向量BK与平面AEF所成角的余弦值,由此能求出平面AEF与平面ACD所成二面角的正弦值的取值范围.
解答  解:由题意把正四面体A-BCD放到正方体BK内,
解:由题意把正四面体A-BCD放到正方体BK内,
则平面ACD与平面AEF所成角的正弦值等于平面ACD的法向量BK与平面AEF所成角的余弦值,
问题等价于平面AEF绕AE转动,
当平面ACD与平面AEF所成角等于BK与AE夹角时,
平面AEF与平面ACD所成二面角的正弦值取最小值,
此时该正弦值为$\frac{\sqrt{2}}{3}$;
当平面AEF与BK平行时,所成角为0°,
此时正弦值为1.
∴平面AEF与平面ACD所成二面角的正弦值的取值范围为[$\frac{\sqrt{2}}{3}$,1].
故答案为:[$\frac{\sqrt{2}}{3}$,1].
点评 本题考查二面角的正弦值的取值范围的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,以Ox轴为始边做锐角α和钝角β,它们的终边分别与单位圆相交于A、B两点,已知A、B的纵坐标分别为$\frac{{\sqrt{5}}}{5}$,$\frac{{\sqrt{10}}}{10}$.
如图,在平面直角坐标系xOy中,以Ox轴为始边做锐角α和钝角β,它们的终边分别与单位圆相交于A、B两点,已知A、B的纵坐标分别为$\frac{{\sqrt{5}}}{5}$,$\frac{{\sqrt{10}}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
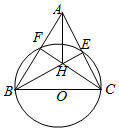 如图,△ABC中,以BC为直径的⊙O分别交AC,AB于点E,F,BE,CF交于点H.求证:
如图,△ABC中,以BC为直径的⊙O分别交AC,AB于点E,F,BE,CF交于点H.求证:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 8 | 15 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | x | 3 | 2 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 10 | 10 | y | 3 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com