
【题目】如图,在四面体A-BCD中,AD![]() 平面BCD,BC
平面BCD,BC![]() CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
(I)证明:PQ//平面BCD;
(II)若异面直线PQ与CD所成的角为![]() ,二面角C-BM-D的大小为
,二面角C-BM-D的大小为![]() ,求cos
,求cos![]() 的值。
的值。
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】

试题分析:(1)连![]() 并延长交
并延长交![]() 于
于![]() ,连
,连![]() 过
过![]() 作
作![]() 交
交![]() 于
于![]() ,由三角形中位线定理以及全等三角形的性质可得
,由三角形中位线定理以及全等三角形的性质可得![]() ,结合条件
,结合条件![]() 推导出
推导出![]() ,由此能证明
,由此能证明![]() 平面
平面![]() ;(2)过
;(2)过![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,连
,连![]() ,可证明
,可证明![]() 平面
平面![]() ,可得
,可得![]() ,即为二面角
,即为二面角![]() 的平面角,由直角三角形的性质可求出
的平面角,由直角三角形的性质可求出![]() 的值.
的值.
试题解析:(1)证明:如图,连AP并延长交BD于E,连CE,
过M作MN∥BD交AP于N,则AN=NE,NP=PE.
故AP=3PE,从而PQ∥CE.
因PQ平面BCD,CE平面BCD,
故PQ∥平面BCD.
(2)解:过C作CF⊥BD于F,作CR⊥BM于R,连FR.
因AD⊥平面BCD,故平面ABD⊥平面BCD,
故CF⊥平面ABD,因此CF⊥BM,从而BM⊥平面RCF,
所以∠CRF=θ即为二面角C﹣BM﹣D的平面角.
因PQ∥CE,故∠DCE=45°,因此CE即为∠BCD的角平分线.
由 (1)知DE=2MN=2EB,故DC=2BC,
从而BC=1,![]() .
.
由题意知BC⊥平面ACD,故BC⊥CM.
由题意知![]() ,故
,故![]() .
.
所以![]() =
=![]() ,从而
,从而![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、二面角及其平面角,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,AB⊥AD,E是AB的中点,AB=AD=PA=PB=2,BC=1,PC= ![]() .
. 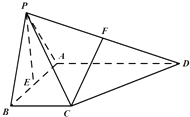
(1)求证:CF∥平面PAB;
(2)求证:PE⊥平面ABCD;
(3)求二面角B﹣PA﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角坐标![]() 中,设椭圆
中,设椭圆![]() :
:![]() 的左右两个焦点分别为
的左右两个焦点分别为![]() ,
,![]() ,过右焦点
,过右焦点![]() 且与
且与![]() 轴垂直的直线
轴垂直的直线![]() 与椭圆
与椭圆![]() 相交,其中一个交点为
相交,其中一个交点为![]() .
.
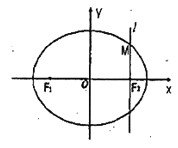
(1)求椭圆![]() 的方程;
的方程;
(2)已知![]() ,
,![]() 经过点
经过点![]() 且斜率为
且斜率为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 有两个不同的
有两个不同的![]() 和
和![]() 交点,请问是否存在常数
交点,请问是否存在常数![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出
共线?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在空间中,设m,n为两条不同直线,α,β为两个不同平面,则下列命题正确的是( )
A. 若m∥α且α∥β,则m∥β
B. 若α⊥β,mα,nβ,则m⊥n
C. 若m⊥α且α∥β,则m⊥β
D. 若m不垂直于α,且nα,则m必不垂直于n
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=m(x﹣2m)(x+m+3),g(x)=2x﹣2,若同时满足条件:
①x∈R,f(x)<0或g(x)<0;
②x∈(﹣∞,﹣4),f(x)g(x)<0.
则m的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C:(5﹣m)x2+(m﹣2)y2=8(m∈R)
(1)若曲线C是焦点在x轴点上的椭圆,求m的取值范围;
(2)设m=4,曲线c与y轴的交点为A,B(点A位于点B的上方),直线y=kx+4与曲线c交于不同的两点M、N,直线y=1与直线BM交于点G.求证:A,G,N三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/oC | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另3天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()
(2)若由线性回归方程得到的估计数据与所选出的两组检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠.
(参考公式,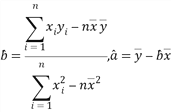 )
)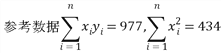
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的图形是由一个半径为2的圆和两个半径为1的半圆组成,它们的圆心分别为O,O1 , O2 . 动点P从A点出发沿着圆弧按A→O→B→C→A→D→B的路线运动(其中A,O1 , O,O2 , B五点共线),记点P运动的路程为x,设y=|O1P|2 , y与x的函数关系为y=f(x),则y=f(x)的大致图象是( ) 
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com