
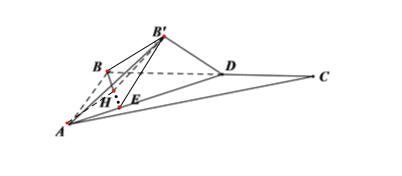
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,D为线段BC(端点除外)上一动点.现将
,D为线段BC(端点除外)上一动点.现将![]() 沿线段AD折起至
沿线段AD折起至![]() ,使二面角
,使二面角![]() 的大小为120°,则在点D的移动过程中,下列说法错误的是( )
的大小为120°,则在点D的移动过程中,下列说法错误的是( )

A.不存在点![]() ,使得
,使得![]()
B.点![]() 在平面
在平面![]() 上的投影轨迹是一段圆弧
上的投影轨迹是一段圆弧
C.![]() 与平面
与平面![]() 所成角的余弦值的取值范围是
所成角的余弦值的取值范围是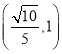
D.线段![]() 的最小值是
的最小值是![]()
【答案】D
【解析】
过点B作AD的垂线,交AD于点E,连接![]() ,
,![]() ,过点
,过点![]() 作BE的垂线,交BE于点H,进而证明
作BE的垂线,交BE于点H,进而证明![]() 平面ABC,即
平面ABC,即![]() 在平面ABC上的投影为点H,连接CH,假设
在平面ABC上的投影为点H,连接CH,假设![]() ,则
,则![]() ,即可判断A;由
,即可判断A;由![]() ,可判断点E的轨迹,进而判断B;连接AH,则
,可判断点E的轨迹,进而判断B;连接AH,则![]() 与平面ABC所成的角为
与平面ABC所成的角为![]() ,由相似可得
,由相似可得![]() ,设
,设![]() ,可得
,可得![]() 的范围,即可得
的范围,即可得![]() 的范围,即可判断C;设
的范围,即可判断C;设![]() ,在
,在![]() 中利用余弦定理求解,即可判断D.
中利用余弦定理求解,即可判断D.
过点B作AD的垂线,交AD于点E,连接![]() ,
,![]() ,过点
,过点![]() 作BE的垂线,交BE于点H,易知
作BE的垂线,交BE于点H,易知![]() ,则
,则![]() 平面
平面![]() ,所以
,所以![]() 为二面角
为二面角![]() 的平面角的补角,即
的平面角的补角,即![]() ,所以
,所以![]() ,即H为BE的中点,易知平面
,即H为BE的中点,易知平面![]() 平面
平面![]() ,又
,又![]() ,所以
,所以![]() 平面ABC,所以
平面ABC,所以![]() 在平面ABC上的投影为点H,
在平面ABC上的投影为点H,
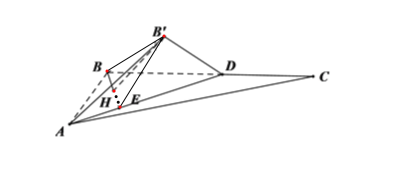
对于选项A,若![]() ,连接CH,则
,连接CH,则![]() ,而这是不可能成立的,故A正确;
,而这是不可能成立的,故A正确;
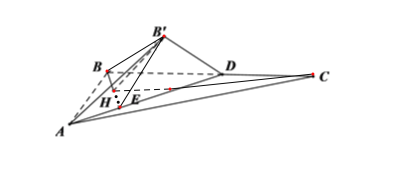
对于选项B,因为![]() ,所以点E的轨迹为以AB为直径的一段圆弧,又H为BE的中点,所以点H的轨迹也为一段圆弧,故B正确;
,所以点E的轨迹为以AB为直径的一段圆弧,又H为BE的中点,所以点H的轨迹也为一段圆弧,故B正确;
对于选项C,连接AH,则![]() 与平面ABC所成的角为
与平面ABC所成的角为![]() ,设
,设![]() ,则
,则![]() ,所以由
,所以由![]() ,得
,得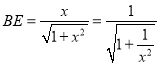 ,所以
,所以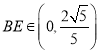 ,所以
,所以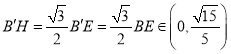 ,所以
,所以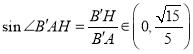 ,所以
,所以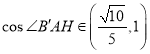 ,故C正确;
,故C正确;
对于选项D,设![]() ,则
,则![]() ,
,![]() ,
,
![]()
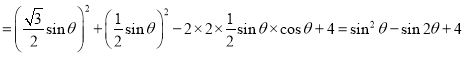
![]() ,
,
其中![]() ,故
,故![]() ,故D错误,
,故D错误,
故选:D


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,AB是圆O:x2+y2=1的直径,且点A在第一象限;圆O1:(x﹣a)2+y2=r2(a>0)与圆O外离,线段AO1与圆O1交于点M,线段BM与圆O交于点N,且![]() ,则a的取值范围为_______.
,则a的取值范围为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】桥牌是一种高雅、文明、竞技性很强的智力性游戏.近年来,在中国桥牌协会“桥牌进校园”活动的号召下,全国各地中小学纷纷积极加入到青少年桥牌推广的大营中.为了了解学生对桥牌这项运动的兴趣,某校从高一学生中随机抽取了200名学生进行调查,经统计男生与女生的人数之比为2:3,男生中有50人对桥牌有兴趣,女生中有20人对桥牌不感兴趣.
(1)完成2×2列联表,并回答能否有![]() 的把握认为“该校高一学生对桥牌是否感兴趣与性别有关”?
的把握认为“该校高一学生对桥牌是否感兴趣与性别有关”?
感兴趣 | 不感兴趣 | 合计 | |
男 | 50 | —— | —— |
女 | —— | 20 | —— |
合计 | —— | —— | 200 |
(2)从被调查的对桥牌有兴趣的学生中利用分层抽样抽取6名学生,再从6名学生中抽取2名学生作为桥牌搭档参加双人赛.求抽到一名男生与一名女生的概率.
附:参考公式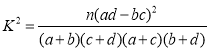 ,其中
,其中![]() .
.
临界值表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为支援武汉的防疫,某医院职工踊跃报名,其中报名的医生18人,护士12人,医技6人,根据需要,从中抽取一个容量为n的样本参加救援队,若采用系统抽样和分层抽样,均不用剔除人员.当抽取n+1人时,若采用系统抽样,则需剔除1个报名人员,则抽取的救援人员为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 过点
过点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如图,设直线![]() 与圆
与圆![]() 相切与点
相切与点![]() ,与椭圆
,与椭圆![]() 相切于点
相切于点![]() ,当
,当![]() 为何值时,线段
为何值时,线段![]() 长度最大?并求出最大值.
长度最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的准线经过点
的准线经过点![]() ,过
,过![]() 的焦点
的焦点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,
,![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,则下列结论正确的是( )
两点,则下列结论正确的是( )
A.![]() B.
B.![]() 的最小值为16
的最小值为16
C.四边形![]() 的面积的最小值为64D.若直线
的面积的最小值为64D.若直线![]() 的斜率为2,则
的斜率为2,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】任取一个自然数,如果它是偶数,我们就把它除以2,如果它是奇数,我们就把它乘3再加上1,在这样的变换下,我们就得到一个新的自然数.如果反复使用这个变换,我们就会得到一串自然数,最终我们都会陷在4→2→1这个循环中,这就是世界数学名题“3x+1问题”.如图所示的程序框图的算法思路源于此,执行该程序框图,若N=6,则输出的i=( )
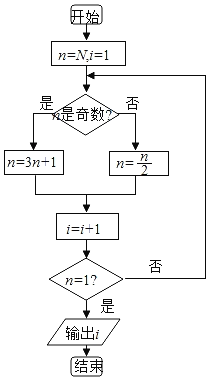
A.6B.7C.8D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a=2![]() ,_______,求△ABC的周长l的范围.
,_______,求△ABC的周长l的范围.
在①![]() (﹣cos
(﹣cos![]() ,sin
,sin![]() ),
),![]() (cos
(cos![]() ,sin
,sin![]() ),且
),且![]()
![]() ,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x
,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x![]() )
)![]() ,f(A)
,f(A)![]()
注:这三个条件中任选一个,补充在上面问题中并对其进行求解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com