
 将一圆的六个等分点分成两组相间的三点﹐它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星﹐如图所示的正六角星是以原点O为中心﹐其中
将一圆的六个等分点分成两组相间的三点﹐它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星﹐如图所示的正六角星是以原点O为中心﹐其中| x |
| y |
| x |
| y |
| A、2 | B、3 | C、4 | D、5 |
| OA |
| x |
| OB |
| OF |
| FB |
| y |
| x |
| x |
| y |
| OC |
| OF |
| FC |
| y |
| x |
| x |
| y |
| OD |
| OF |
| FE |
| ED |
| y |
| x |
| OC |
| y |
| x |
| y |
| x |
| x |
| y |
| OE |
| OF |
| FE |
| y |
| x |
| x |
| y |
| OF |
| y |


 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
| b2 |
| a2+2c2 |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、一个平面的面积可以是16cm2 |
| B、空间三点可以确定一个平面 |
| C、平面α与平面β相交于线段AB |
| D、两条相交直线可以确定一个平面 |
查看答案和解析>>
科目:高中数学 来源: 题型:
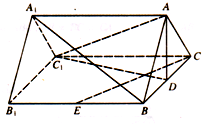 如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D,E分别为BC,BB1的中点,四边形B1BCC1是边长为6的正方形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com