
【题目】已知非单调数列{an}是公比为q的等比数列,a1=![]() ,其前n项和为Sn(n∈N*),且满足S3+a3,S5+a5,S4+a4成等差数列.
,其前n项和为Sn(n∈N*),且满足S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式和前n项和Sn;
(2)bn=![]() +
+![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
【答案】(1)![]() ,
,![]() ;(2)见解析
;(2)见解析
【解析】
(1)由已知S3+a3,S5+a5,S4+a4成等差数列构造方程解出公比q,代入等比数列的通项公式和前n项和公式可求出an与Sn;(2)由(1)求出bn=(-1)nn2+![]() ,前半部分利用分类法和等差数列求和公式求和,后半部分利用错位相减法和等比数列前n项和公式求和.
,前半部分利用分类法和等差数列求和公式求和,后半部分利用错位相减法和等比数列前n项和公式求和.
(1)∵S3+a3,S5+a5,S4+a4成等差数列,
∴2(S5+a5)=(S3+a3)+(S4+a4)
∴a3=4a5,q2=![]() ,q=-
,q=-![]() ,
,
an=![]() ·
·![]() n-1,
n-1,
∴Sn=1-![]() n.
n.
(2)bn=(-1)nn2Sn+![]() =(-1)nn2
=(-1)nn2![]() +
+![]() =(-1)nn2+
=(-1)nn2+![]() .
.
设(-1)nn2的前n项和为Hn,![]() 的前n项和为Qn
的前n项和为Qn
①当n为偶数时,
Hn=-12+22-32+42+…-(n-1)2+n2=1+2+3+4+…+n-1+n=![]() ,
,
Qn=1×![]() +2×
+2×![]() 2+…+n×
2+…+n×![]() n ①
n ①
![]() Qn=1×
Qn=1×![]() 2+…+(n-1)×
2+…+(n-1)×![]() n+n×
n+n×![]() n+1 ②
n+1 ②
①-②得,![]() Qn=
Qn=![]() +
+![]() 2+…+
2+…+![]() n-n×
n-n×![]() n+1=1-
n+1=1-![]() ,
,
∴Qn=2-![]()
∴Tn=Hn+Qn=![]() +2-
+2-![]() =
=![]() -
-![]()
②当n为奇数时,
Hn=![]() -n2=-
-n2=-![]() ,
,
∴Qn=2-![]()
∴Tn=Hn+Qn=-![]() +2-
+2-![]() =-
=-![]() -
-![]()
综合①②,∴Tn=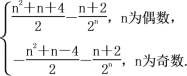


科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1且an﹣an﹣1=3×(![]() )n﹣2(n≥2,n∈N*).
)n﹣2(n≥2,n∈N*).
(1)求数列{an}的通项公式:
(2)若对任意的n∈N*,不等式1≤man≤5恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数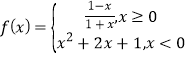 ,函数g(x)=f(1-x)-kx+k-
,函数g(x)=f(1-x)-kx+k-![]() 恰有三个不同的零点,则k的取值范围是( )
恰有三个不同的零点,则k的取值范围是( )
A. (-2-![]() ,0]∪
,0]∪![]() B. (-2+
B. (-2+![]() ,0]∪
,0]∪![]()
C. (-2-![]() ,0]∪
,0]∪![]() D. (-2+
D. (-2+![]() ,0]∪
,0]∪![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A,B两城相距100 km,在两地之间距A城x km处的D地建一核电站给A,B两城供电.为保证城市安全,核电站与城市距离不得少于10 km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数λ=0.25.若A城供电量为20亿度/月,B城为10亿度/月.
(1)求x的取值范围;
(2)把月供电总费用y表示成x的函数;
(3)核电站建在距A城多远,才能使供电费用最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
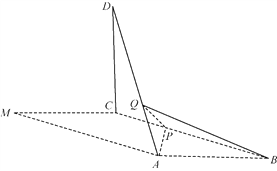
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为折痕将△
为折痕将△![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)![]() 为线段
为线段![]() 上一点,
上一点,![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com