
分析 (1)利用初等函数的性质、弱减函数的定义,判断$f(x)=\frac{1}{{\sqrt{1+x}}}$是[0,+∞)上的弱减函数.
(2)根据题意可得$\left\{\begin{array}{l}a≤{({\frac{x}{{\sqrt{1+x}}}})_{min}}\\ \frac{a+4}{2}≥{({\frac{x}{{\sqrt{1+x}}}})_{max}}\end{array}\right.$,再利用函数的单调性求得函数的最值,可得a的范围.
(3)根据题意,当x∈(0,3]时,方程$1-\frac{1}{{\sqrt{1+x}}}=k|x|$只有一解,分离参数k,换元利用二次函数的性质,求得k的范围.
解答 解:(1)由初等函数性质知,$f(x)=\frac{1}{{\sqrt{1+x}}}$在[0,+∞)上单调递减,
而$xf(x)=\frac{x}{{\sqrt{1+x}}}=\frac{(x+1)-1}{{\sqrt{1+x}}}=\sqrt{1+x}-\frac{1}{{\sqrt{1+x}}}$在[0,+∞)上单调递增,
所以$f(x)=\frac{1}{{\sqrt{1+x}}}$是[0,+∞)上的弱减函数.
(2)不等式化为$a≤\frac{x}{{\sqrt{1+x}}}≤\frac{a+4}{2}$在x∈[1,3]上恒成立,则$\left\{\begin{array}{l}a≤{({\frac{x}{{\sqrt{1+x}}}})_{min}}\\ \frac{a+4}{2}≥{({\frac{x}{{\sqrt{1+x}}}})_{max}}\end{array}\right.$,
而$y=\frac{x}{{\sqrt{1+x}}}$在[1,3]单调递增,∴$\frac{x}{\sqrt{1+x}}$的最小值为$\frac{1}{2}$,$\frac{x}{\sqrt{1+x}}$的最大值为 $\frac{3}{2}$,
∴$\left\{\begin{array}{l}{a≤\frac{1}{2}}\\{\frac{a+4}{2}≥\frac{3}{2}}\end{array}\right.$,∴a∈[-1,$\frac{1}{2}$].
(3)由题意知方程$1-\frac{1}{{\sqrt{1+x}}}=k|x|$在[0,3]上有两个不同根,
①当x=0时,上式恒成立;
②当x∈(0,3]时,则由题意可得方程$1-\frac{1}{{\sqrt{1+x}}}=k|x|$只有一解,
根据 $k=\frac{1}{x}(1-\frac{1}{{\sqrt{1+x}}})=\frac{1}{x}•\frac{{\sqrt{1+x}-1}}{{\sqrt{1+x}}}=\frac{1}{x}•\frac{x}{{\sqrt{1+x}•(\sqrt{1+x}+1)}}=\frac{1}{{{{(\sqrt{1+x})}^2}+\sqrt{1+x}}}$,
令$t=\sqrt{1+x}$,则t∈(1,2],
方程化为$k=\frac{1}{{{t^2}+t}}$在t∈(1,2]上只有一解,所以$k∈[\frac{1}{6},\frac{1}{2})$.
点评 本题主要考查新定义,函数的单调性的应用,函数的零点与方程根的关系,属于中档题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{364}$ | B. | $\frac{1}{121}$ | C. | $\frac{120}{121}$ | D. | $\frac{363}{364}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
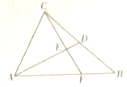 如图△ABC,点D是BC中点,$\overrightarrow{AF}$=2$\overrightarrow{FB}$,CF和AD交于点E,设$\overrightarrow{AD}$=a,$\overrightarrow{AB}$=b.
如图△ABC,点D是BC中点,$\overrightarrow{AF}$=2$\overrightarrow{FB}$,CF和AD交于点E,设$\overrightarrow{AD}$=a,$\overrightarrow{AB}$=b.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-[x]≥0 | |
| B. | x-[x]<1 | |
| C. | 令f(x)=x-[x],对任意实数x,f(x+1)=f(x)恒成立 | |
| D. | 令f(x)=x-[x],对任意实数x,f(-x)=f(x)恒成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
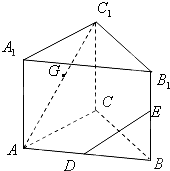 如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.
如图,在正三棱柱ABC-A1B1C1中,D、E、G分别是AB、BB1、AC1的中点,AB=BB1=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com