
 为了调查一款项链的销售数量x(件)与销售利润y(万元)之间的相关关系,某公司的市场专员作出调查并将结果统计如表所示:
为了调查一款项链的销售数量x(件)与销售利润y(万元)之间的相关关系,某公司的市场专员作出调查并将结果统计如表所示:| x(件) | 3 | 4 | 5 | 6 | 8 | 10 |
| y(万元) | 3 | 2 | 4 | 6 | 7 | 8 |
分析 (Ⅰ)利用所给数据作出x,y的散点图;
(Ⅱ)分别求出直线方程,即可得出结论.
解答 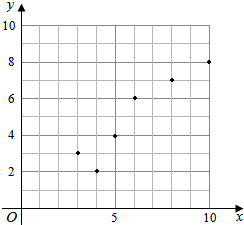 解:(Ⅰ)x,y的散点图如图;
解:(Ⅰ)x,y的散点图如图;
(Ⅱ)$\overline{x}$=6,$\overline{y}$=5,∴b=$\frac{9+8+20+36+56+80-6×6×5}{9+16+25+36+64+100-6×36}$=$\frac{29}{34}$,
a=5-6×$\frac{29}{34}$=-$\frac{2}{17}$.
根据如表中的数据(6,6)和(8,7)求得的直线方程为y=$\frac{1}{2}$x+3,
∴b′<b,a′>a.
点评 本题考查散点图,线性回归方程,考查学生的计算能力,属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 16π2 | B. | 4π2 | C. | 2π2 | D. | π2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
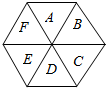 如图,一个正六边形分为6个区域A、B、C、D、E、F,现给这6个区域着色,要求同一区域染同一种颜色,相邻的两个区域不得使用同一颜色,现有红,黄,蓝,绿四种颜色可供选择,且A必须涂红色,则有多少种不同的着色方法?
如图,一个正六边形分为6个区域A、B、C、D、E、F,现给这6个区域着色,要求同一区域染同一种颜色,相邻的两个区域不得使用同一颜色,现有红,黄,蓝,绿四种颜色可供选择,且A必须涂红色,则有多少种不同的着色方法?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥b,且a?β,则α∥β | B. | 若α∥β,则a∥b | ||
| C. | 若a∥b,且a?β,则a∥β | D. | 若a∥β,则a∥b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com