
【题目】很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以![]() 再加1;如果它是偶数,则将它除以
再加1;如果它是偶数,则将它除以![]() ;如此循环,最终都能够得到
;如此循环,最终都能够得到![]() .下图为研究“角谷猜想”的一个程序框图.若输入
.下图为研究“角谷猜想”的一个程序框图.若输入![]() 的值为
的值为![]() ,则输出i的值为( )
,则输出i的值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某啤酒厂要将一批鲜啤酒用汽车从所在城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,运费由厂家承担.若厂家恰能在约定日期(×月×日)将啤酒送到,则城市乙的销售商一次性支付给厂家40万元;若在约定日期前送到,每提前一天销售商将多支付给厂家2万;若在约定日期后送到,每迟到一天销售商将少支付给厂家2万元.为保证啤酒新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送.已知下表内的信息:
汽车行驶路线 | 在不堵车的情况下到达城市乙所需时间(天) | 在堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
公路1 | 1 | 4 |
| 2 |
公路2 | 2 | 3 |
| 1 |
(1)记汽车选择公路1运送啤酒时厂家获得的毛收入为X(单位:万元),求X的分布列和EX;
(2)若![]() ,
,![]() ,选择哪条公路运送啤酒厂家获得的毛收人更多?
,选择哪条公路运送啤酒厂家获得的毛收人更多?
(注:毛收入=销售商支付给厂家的费用-运费).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,如图是易经八卦(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成("![]() "表示一根阳线,"
"表示一根阳线,"![]() "表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.
"表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有两根阳线,四根阴线的概率为_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若曲线![]() 在点(1,0)处的切线为l : x+y-1=0,求a,b的值;
在点(1,0)处的切线为l : x+y-1=0,求a,b的值;
(3)若![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 图像上有动点
图像上有动点![]() ,函数
,函数![]() 图像上有动点
图像上有动点![]() .若
.若![]() 两点同时从纵坐标
两点同时从纵坐标![]() 的初始位置出发,沿着各自函数图像向右上方运动至
的初始位置出发,沿着各自函数图像向右上方运动至![]() 两点的纵坐标值再次相等,且始终满足
两点的纵坐标值再次相等,且始终满足![]() ,则在此运动过程中
,则在此运动过程中![]() 两点的距离
两点的距离![]() 的取值范围是______.
的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者,为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据:
年底,湖北省武汉市等多个地区陆续出现感染新型冠状病毒肺炎的患者,为及时有效地对疫情数据进行流行病学统计分析,某地研究机构针对该地实际情况,根据该地患者是否有武汉旅行史与是否有确诊病例接触史,将新冠肺炎患者分为四类:有武汉旅行史(无接触史),无武汉旅行史(无接触史),有武汉旅行史(有接触史)和无武汉旅行史(有接触史),统计得到以下相关数据:
有接触史 | 无接触史 | 总计 | |
有武汉旅行史 |
| ||
无武汉旅行史 |
| ||
总计 |
|
|
(1)请将上面列联表填写完整,并判断能否在犯错误的概率不超过![]() 的前提下,认为有武汉旅行史与有确诊病例接触史有关系?
的前提下,认为有武汉旅行史与有确诊病例接触史有关系?
(2)已知在无武汉旅行史的![]() 名患者中,有
名患者中,有![]() 名无症状感染者.现在从无武汉旅行史的
名无症状感染者.现在从无武汉旅行史的![]() 名患者中,选出
名患者中,选出![]() 名进行病例研究,求
名进行病例研究,求![]() 人中至少有
人中至少有![]() 名是无症状感染者的概率.
名是无症状感染者的概率.
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: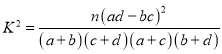 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
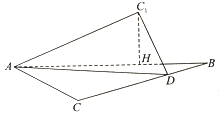
【题目】如图,在等腰![]() 中,斜边
中,斜边![]() ,
,![]() 为直角边
为直角边![]() 上的一点,将
上的一点,将![]() 沿直线
沿直线![]() 折叠至
折叠至![]() 的位置,使得点
的位置,使得点![]() 在平面
在平面![]() 外,且点
外,且点![]() 在平面
在平面![]() 上的射影
上的射影![]() 在线段
在线段![]() 上设
上设![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com