
����Ŀ����ȫ�濹���¹ڷ���������һ����ʱ�ڣ����н����������ͣ�β�ͣѧ���Ŀںţ�����ѧ������ѧϰ.ijУ��ѧ��ʦΪ�˵������ѧ����ѧ�ɼ�������ѧϰʱ��֮�����ع�ϵ���Ը����꼶���ѡȡ45��ѧ�����и����ʾ�������ÿ������ѧϰ��ѧʱ�䲻����5Сʱ����19�ˣ����µ����У��ڼ�⿼������ѧƽ���ɼ�����120�ֵ�ռ![]() ��ͳ�Ƴɼ���õ�����
��ͳ�Ƴɼ���õ�����![]() ��������
��������
����������120�� | ��������120�� | �ϼ� | |
����ѧϰʱ�䲻����5Сʱ | 4 | 19 | |
����ѧϰʱ�䲻��5Сʱ | |||
�ϼ� | 45 |
��1�����������![]() �����������ж��Ƿ���99%�İ�����Ϊ������ѧ������ѧ�ɼ���ѧ������ѧϰʱ���йء���
�����������ж��Ƿ���99%�İ�����Ϊ������ѧ������ѧ�ɼ���ѧ������ѧϰʱ���йء���
��2���ٰ��շֲ�����ķ����������������дӷ���������120�ֺͷ�������120�ֵ�����ѧ���г�ȡ9��ѧ������鵽����120����ÿ������ѧϰʱ�䲻��5Сʱ��������![]() ����
����![]() �ķֲ��У��������������ʽ��ʾ����
�ķֲ��У��������������ʽ��ʾ����
������Ƶ����Ϊ���ʣ���ȫУ�����ôμ����ѧ�ɼ�������120�ֵ�ѧ���������ȡ20�ˣ�����Щ����ÿ������ѧϰʱ�䲻����5Сʱ�������������ͷ���.
��������ٽ�ֵ�����ο���
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���ο���ʽ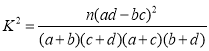 ����
����![]() ��
��
���𰸡���1���������������99%�İ�����Ϊ������ѧ������ѧ�ɼ���ѧ������ѧϰʱ���й�����2�����������������![]() ������
������![]()
��������
��1��������������������ݼ����жϣ�
��2�����÷ֲ�����ɵ�![]() ��ȡֵ�������õ����ʣ��г��ֲ��У����ݷ���֪
��ȡֵ�������õ����ʣ��г��ֲ��У����ݷ���֪![]() ������������뷽��.
������������뷽��.
��1��
����������120�� | ��������120�� | �ϼ� | |
����ѧϰʱ�䲻����5Сʱ | 15 | 4 | 19 |
����ѧϰʱ�䲻��5Сʱ | 10 | 16 | 26 |
�ϼ� | 25 | 20 | 45 |
![]()
![]() ��99%�İ�����Ϊ������ѧ������ѧ�ɼ���ѧ������ѧϰʱ���й���.
��99%�İ�����Ϊ������ѧ������ѧ�ɼ���ѧ������ѧϰʱ���й���.
��2�����ɷֲ����֪����Ҫ�Ӳ���120�ֵ�ѧ���г�ȡ![]() �ˣ�
�ˣ�
![]() �Ŀ���ȡֵΪ0��1��2��3��4��
�Ŀ���ȡֵΪ0��1��2��3��4��
![]() ��
��![]() ��
��![]()
![]() ����
����
���ԣ�![]() �ķֲ��У�
�ķֲ��У�
|
|
|
|
|
|
|
|
|
|
|
|
�ڴ�ȫУ������120�ֵ�ѧ���������ȡ1�ˣ�����ÿ������ʱ�䲻����5Сʱ�ĸ���Ϊ![]() �����ȫУ������120�ֵ�ѧ���������ȡ20�ˣ���Щ����ÿ������ѧϰʱ�䲻����5Сʱ������Ϊ
�����ȫУ������120�ֵ�ѧ���������ȡ20�ˣ���Щ����ÿ������ѧϰʱ�䲻����5Сʱ������Ϊ![]() ����
����![]() ��
��
��![]() ��
��![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ĵȱ�����![]() ���㣺
���㣺![]() .��
.��![]() ��
��![]() ��
��![]() �ĵȲ�����.������
�ĵȲ�����.������![]() ���㣺
���㣺![]() ��
��![]() ��
��![]() .
.
��1��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ��������
��������![]() Ϊ�ȱ����У���
Ϊ�ȱ����У���![]() ��ֵ��
��ֵ��
��3����![]() ����
����![]() ����
Ϊ����![]() ����С���
����С���![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ʱ������
ʱ������![]() ������
������![]() ����������
����������
��2������![]() ʱ��
ʱ��![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]()
![]() ������
������![]() ��
��![]() ������A��B�IJ�Ϊ
������A��B�IJ�Ϊ![]() ��A��B֮��ľ���Ϊ
��A��B֮��ľ���Ϊ![]() ��
��
��I����![]() ����д�����п��ܵ�A��B��
����д�����п��ܵ�A��B��
��II��![]() ��֤����
��֤����
��i��![]() ��
��
��ii��![]()
![]()
![]() ��������������һ����ż����
��������������һ����ż����
��III����![]() ��
��![]() ����m��
����m��![]() ����Ϊ��������Ԫ�أ���P��������Ԫ�ؼ�����ƽ��ֵΪ
����Ϊ��������Ԫ�أ���P��������Ԫ�ؼ�����ƽ��ֵΪ![]() ��֤����
��֤����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() .
.
��1����![]() ʱ����
ʱ����![]() ǡ��һ����㣬��ʵ��
ǡ��һ����㣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2����![]() ʱ��
ʱ��![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����xlnx��x+1��g��x����ex��ax��a��R��
������f��x������Сֵ��
������g��x����1��R�Ϻ��������a��ֵ��
������֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѡ�⣩����ʵ��![]() ����
����![]() ����
����
A. ![]() ����Сֵ4B.
����Сֵ4B. ![]() ����Сֵ
����Сֵ![]()
C. ![]() �����ֵ
�����ֵ![]() D.
D. ![]() ����Сֵ
����Сֵ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �Ǻ���
�Ǻ���![]() �������ڵ�һ���Ӽ���������
�������ڵ�һ���Ӽ���������![]() ��ʹ��
��ʹ��![]() ���������
���������![]() ��
��![]() ��һ���������㡱��Ҳ��
��һ���������㡱��Ҳ��![]() ������
������![]() �ϴ��ڲ����㣮
�ϴ��ڲ����㣮
�躯��![]() ��
��![]() ��
��
��1����![]() ������
������![]() �IJ����㣻
�IJ����㣻
��2��������![]() ��
��![]() �ϲ����ڲ����㣬��ʵ��
�ϲ����ڲ����㣬��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
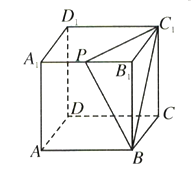
����Ŀ����ͼ��ʾ�����ⳤΪ2��������![]() �У�
��![]() �����P������
�����P������![]() �������
�������![]() ƽ�еĽ��棬���������Ϊ__________.
ƽ�еĽ��棬���������Ϊ__________.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com