
(Ⅰ)(20分)在复数范围内解方程 (i为虚数单位)
(i为虚数单位)
(Ⅱ)设z是虚数,ω=z+ 是实数,且-1<ω<2
是实数,且-1<ω<2
(1)求|z|的值及z的实部的取值范围;(10分)
(2)设u= ,求证:u为纯虚数;(5分)
,求证:u为纯虚数;(5分)
(3)求ω-u2的最小值,(5分)
(Ⅰ)原方程化简为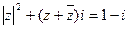 ,
,
设z=x+yi(x、y∈R),代入上述方程得 x2+y2+2xi="1-i,"
∴x2+y2=1且2x=-1,解得x=-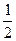 且y=±
且y=±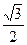 ,
,
∴原方程的解是z=-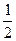 ±
±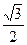 i.
i.
(Ⅱ)(1)设z=a+bi(a、b∈R,b≠0),
则ω=a+bi+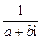 =(a+
=(a+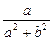 )+(b-
)+(b-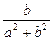 )i
)i
∵ω是实数,∴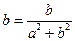 ,又∵b≠0,∴a2+b2=1,即|z|=1
,又∵b≠0,∴a2+b2=1,即|z|=1
∵ω=2a,-1<ω<2,∴z的实部的取值范围是(-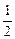 ,1)
,1)
(2)证明:u= =
=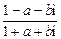 =
=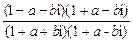 =
=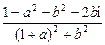
由(1)知a2+b2=1,∴u=-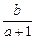 I,又∵a∈(-
I,又∵a∈(-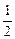 ,1),b≠0,
,1),b≠0,
∴u为纯虚数
(3)解:ω-u2=2a+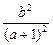 =2a+
=2a+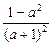 =2a-
=2a-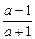
=2a-1+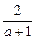 =2[(a+1)+
=2[(a+1)+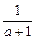 ]-3
]-3
∵a∈(-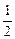 ,1),∴a+1>0,
,1),∴a+1>0,
∴(a+1)+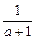 ≥2(当a+1=
≥2(当a+1=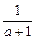 ,即a=0时,上式取等号.)
,即a=0时,上式取等号.)
∴ω-u2≥2×2-3=1,∴ω-u2的最小值为1.
解析


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com