
【题目】已知椭圆![]() 的左右顶点是双曲线
的左右顶点是双曲线![]() 的顶点,且椭圆
的顶点,且椭圆![]() 的上顶点到双曲线
的上顶点到双曲线![]() 的渐近线的距离为
的渐近线的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 相交于
相交于![]() 两点,与
两点,与![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
![]() 由双曲线的顶点可得
由双曲线的顶点可得![]() ,求出双曲线的渐近线方程,运用点到直线的距离公式可得
,求出双曲线的渐近线方程,运用点到直线的距离公式可得![]() ,即可得到椭圆方程
,即可得到椭圆方程
![]() 设直线
设直线![]() 的方程为
的方程为![]() ,联立双曲线方程,消去
,联立双曲线方程,消去![]() ,运用韦达定理和判别式大于
,运用韦达定理和判别式大于![]() ,结合向量的数量积的坐标表示,求得
,结合向量的数量积的坐标表示,求得![]() 的关系式,再由直线方程和椭圆方程联立,运用韦达定理和弦长公式,计算即可得到所求
的关系式,再由直线方程和椭圆方程联立,运用韦达定理和弦长公式,计算即可得到所求
(1)由题意可知:![]() ,
,
又椭圆![]() 的上顶点为
的上顶点为![]() ,
,
双曲线![]() 的渐近线为:
的渐近线为:![]() ,
,
由点到直线的距离公式有:![]() ,
,
所以椭圆的方程为![]() 。
。
(2)易知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() ,消去
,消去![]() 并整理得:
并整理得:
![]() ,
,
要与![]() 相交于两点,则应有:
相交于两点,则应有:

![]()
设![]() ,
,
则有:![]() ,
,![]() .
.
又![]()
![]()
![]() .
.
又:![]() ,所以有:
,所以有:![]()
![]() ,
,
![]() ,②
,②
将![]() ,代入
,代入![]() ,消去
,消去![]() 并整理得:
并整理得:![]() ,
,
要有两交点,则![]()
![]() .③
.③
由①②③有:![]()
设![]() 、
、![]() .
.
有:![]() ,
,![]()

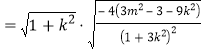 .
.
将![]() 代入有:
代入有:![]()
![]() .
.
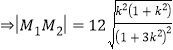 ,令
,令![]() ,
,![]()
令![]()
![]() ,
,![]() .
.
所以![]() 在
在![]() 内恒成立,故函数
内恒成立,故函数![]() 在
在![]() 内单调递增,
内单调递增,
故![]()
![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() 为圆
为圆![]() 的圆心,
的圆心, ![]() 是圆上的动点,点
是圆上的动点,点![]() 在圆的半径
在圆的半径![]() 上,且有点
上,且有点![]() 和
和![]() 上的点
上的点![]() ,满足
,满足![]() ,
, ![]() .
.
(1)当点![]() 在圆上运动时,求点
在圆上运动时,求点![]() 的轨迹方程;
的轨迹方程;
(2)若斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 相切,直线
相切,直线![]() 与(1)中所求点
与(1)中所求点![]() 的轨迹交于不同的两点
的轨迹交于不同的两点![]() ,
, ![]() ,
, ![]() 是坐标原点,且
是坐标原点,且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为矩形,侧棱PA⊥底面ABCD,且PA=AD,E,F分别是线段PA,PD的中点,H在线段AB上.
(1)求证:PC⊥AF;
(2)若平面PBC∥平面EFH,求证H是AB的中点;
(3)若AD=4,AB=2,求点D到平面PAC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asinx﹣ ![]() cosx(a∈R)的图象经过点(
cosx(a∈R)的图象经过点( ![]() ,0).
,0).
(1)求f(x)的最小正周期;
(2)若x∈[ ![]() ,
, ![]() ],求f(x)的取值范围.
],求f(x)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,斜三棱柱ABC﹣A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为 ![]() ,且∠AA1C1为锐角.
,且∠AA1C1为锐角.
(I) 求证:AA1⊥BC1;
(Ⅱ)求锐二面角B﹣AC﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的焦距为
的焦距为 ![]() ,且过点
,且过点 ![]() ,设
,设 ![]() ,
,![]() 是
是 ![]() 上的两个动点,线段
上的两个动点,线段 ![]() 的中点
的中点 ![]() 的横坐标为
的横坐标为 ![]() ,线段
,线段 ![]() 的中垂线交椭圆
的中垂线交椭圆 ![]() 于
于 ![]() ,
,![]() 两点.
两点.
(1)求椭圆 ![]() 的方程;
的方程;
(2)设![]() 点纵坐标为m,求直线
点纵坐标为m,求直线![]() 的方程,并求出
的方程,并求出 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com