
分析 (1)当a=1时,求出函数f(x)的解析式和导函数,利用f′(x)>0,函数单调递增,f′(x)<0,函数单调递减;
(2)当a>0时,求导,利用导数求得函数的单调性,根据单调性求得函数的最小值,利用f′(x0)=0,求得a的值,构造辅助函数g(x)=ex(-x2-x+1),(x>-1),求导,求出函数的g(x)的极大值,由g(x)<g(0)=0,即可证明f(x0)<1.
解答 解:(1)当a=1时,f′(x)=ex-$\frac{1}{{(x+1)}^{2}}$,
∵ex单调递增,-$\frac{1}{{(x+1)}^{2}}$(x>-1)单调递增,
∴f′(x)在(-1,+∞)单调递增,且f′(0)=0,
∴当-1<x<0时,f′(x)<0;当x>0时,f′(x)>0,
故f(x)在(-1,0)单调递减,在(0,+∞)单调递增;
(2)证明:当a>0时,f′(x)=ex-$\frac{a}{{(x+1)}^{2}}$,
∵ex单调递增,-$\frac{a}{{(x+1)}^{2}}$(x>-1)单调递增,
∴f′(x)在(-1,+∞)单调递增.
又f′(2$\sqrt{a}$-1)=${e}^{2\sqrt{a}-1}$-$\frac{a}{{(2\sqrt{a})}^{2}}$>$\frac{1}{e}$-$\frac{1}{4}$,
当x满足-1<x<$\sqrt{a}$时,f′(x)<0,故f′(x)存在唯一零点,设零点为x1,
当x∈(-1,x1)时,f′(x)<0;当x∈(x1,+∞)时,f′(x)>0.
∴f(x)在(-1,x1)单调递减,在(x1,+∞)单调递增,
∴当x=x1时,f(x)取得最小值,由条件可得x1=x0,f(x)的最小值为f(x0).
由于f′(x0)=e x0-$\frac{a}{{{(x}_{0}+1)}^{2}}$=0,
∴a=ex0•(x0+1)2,
f(x0)=ex0-$\frac{{ax}_{0}}{{x}_{0}+1}$=ex0-ex0•x0•(x0+1)=ex0(-x02-x0+1),
设g(x)=ex(-x2-x+1),(x>-1),
则g′(x)=ex(-x2-3x)=-x(x+3)ex,
令g′(x)>0,得-1<x<0;令g′(x)<0,得x>0,
故g(x)在(-1,0)单调递增,(0,+∞)单调递减,g(x)<g(0)=0,
故f(x0)=g(x0)<1.
点评 本题考查导数的综合运用,考查函数的单调性,考查函数的最值,解题的关键是正确求导,并会根据导数求函数的单调性,考查分析和计算能力,属于难题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(文)试卷(解析版) 题型:选择题
设 ,则“
,则“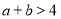 ”是“
”是“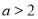 ,且
,且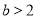 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥S-ABCD中,底面ABCD为正方形,SD⊥面ABCD,点E,F分别为AB,SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,SD⊥面ABCD,点E,F分别为AB,SC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
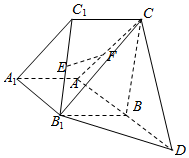 已知三棱柱ABC-A1B1C1中,侧面ABB1A1为正方形,延长AB到D,使得AB=BD,平面AA1C1C⊥平面ABB1A1,A1C1=$\sqrt{2}$AA1,∠C1A1A=$\frac{π}{4}$.
已知三棱柱ABC-A1B1C1中,侧面ABB1A1为正方形,延长AB到D,使得AB=BD,平面AA1C1C⊥平面ABB1A1,A1C1=$\sqrt{2}$AA1,∠C1A1A=$\frac{π}{4}$.查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:选择题
已知直线 的方向向量
的方向向量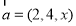 ,直线
,直线 的方向向量
的方向向量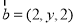 ,若
,若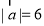 ,且
,且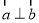 ,则
,则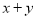 的值是( )
的值是( )
A.-3或1 B.3或-1 C.-3 D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com