
| 3 | 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 3 |
| 4 |
| A、(-∞,12] |
| B、[24,+∞) |
| C、(12,24) |
| D、(-∞,12]∪[24,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 | 4 |
查看答案和解析>>
科目:高中数学 来源:2014届湖北省高二上学期期中考试理科数学试卷(解析版) 题型:填空题
甲、乙两位同学玩游戏,对于给定的实数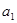 ,按下列方法操作一次产生一个新的实数:由甲、乙同时各抛一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把
,按下列方法操作一次产生一个新的实数:由甲、乙同时各抛一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把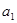 乘以2后再减去12;如果出现一个正面朝上,一个反面朝上,则把
乘以2后再减去12;如果出现一个正面朝上,一个反面朝上,则把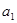 除以2后再加上12,这样就可得到一个新的实数
除以2后再加上12,这样就可得到一个新的实数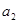 ,对
,对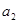 仍按上述方法进行一次操作,又得到一个新的实数
仍按上述方法进行一次操作,又得到一个新的实数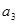 ,当
,当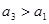 时,甲获胜,否则乙获胜。若甲获胜的概率为
时,甲获胜,否则乙获胜。若甲获胜的概率为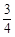 ,则
,则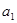 的取值范围是_________.
的取值范围是_________.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年广东省华南师大附中学高一(上)数学试卷(必修3)(解析版) 题型:选择题
 ,则a1的取值范围是( )
,则a1的取值范围是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com