解:(Ⅰ)①A={1,5}不是M={1,2,3,4,5}的一个二元基底.
理由是3≠λ
1×1+λ
2×5;
②A={2,3}是M={1,2,3,4,5}的一个二元基底.
理由是 1=﹣1×2+1×3,2=1×2+0×3,3=0×2+1×3,
4=1×2+1×2,5=1×2+1×3,6=1×3+1×3.
(Ⅱ)不妨设a
1<a
2<a
3<…<a
m,则形如1×a
i+0×a
j(1≤i≤j≤m)的正整数共有m个;
形如1×a
i+1×a
i(1≤i≤m)的正整数共有m个;
形如1×a
i+1×a
j(1≤i≤j≤m)的正整数至多有
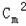
个;
形如﹣1×ai+1×aj(1≤i≤j≤m)的正整数至多有
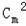
个.
又集合M={1,2,3,…,n}(n∈N*),
含n个不同的正整数,A为集合M的一个m元基底.
故m+m+
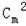
+
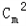
≥n,即m(m+1)≥n
(Ⅲ)由(Ⅱ)可知m(m+1)≥19,所以m≥4.
当m=4时,m(m+1)﹣19=1,
即用基底中元素表示出的数最多重复一个…*
假设A=a
1,a
2,a
3,,a
4为M={1,2,3,…,19}的一个4元基底,
不妨设a
1<a
2<a
3<a
4,则a
4≥10.
当a
4=10时,有a
3=9,这时a
2=8或7.
如果a
2=8,则由1=10﹣9,1=9﹣8,18=9+9,18=10+8,这与结论*矛盾.
如果a
2=7,则a
1=6或5.
易知A={6,7,9,10}和A={5,7,9,10}都不是M={1,2,3,…,19}的4元基底,矛盾.当a
4=11时,有a
3=8,这时a
2=7,a
1=6,
易知A={6,7,8,11}不是M={1,2,3,…,19}的4元基底,矛盾.
当a
4=12时,有a
3=7,这时a
2=6,a
1=5,
易知A={5,6,7,12}不是M={1,2,3,…,19}的4元基底,矛盾.
当a
4=13时,有a
3=6,a
2=5,a
1=4,
易知A={4,5,6,13}不是M={1,2,3,…,19}的4元基底,矛盾.
当a
4=14时,有a
3=5,a
2=4,a
1=3,
易知A={3,4,5,14}不是M={1,2,3,…,19}的4元基底,矛盾.
当a
4=15时,有a
3=4,a
2=3,a
1=2,
易知A={2,3,4,15}不是M={1,2,3,…,19}的4元基底,矛盾.
当a
4=16时,有a
3=3,a
2=2,a
1=1,
易知A={1,2,3,16}不是M={1,2,3,…,19}的4元基底,矛盾.
当a
4≥17时,A均不可能是M的4元基底.
当m=5时,M的一个基底A={1,3,5,9,16}.
综上所述,m的最小可能值为5.

 ,且对任意的b∈M,存在ai,aj∈A(1≤i≤j≤m),使得b=λ1ai+λ2aj(其中λ1,λ2∈{﹣1,0,1}),则称集合A为集合M的一个m元基底.
,且对任意的b∈M,存在ai,aj∈A(1≤i≤j≤m),使得b=λ1ai+λ2aj(其中λ1,λ2∈{﹣1,0,1}),则称集合A为集合M的一个m元基底.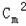 个;
个;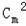 个.
个.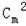 +
+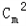 ≥n,即m(m+1)≥n
≥n,即m(m+1)≥n
