
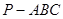 中,
中,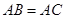 ,
,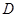 为
为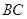 的中点,
的中点,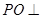 平面
平面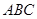 ,垂足
,垂足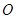 落在线段
落在线段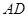 上,已知
上,已知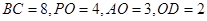 。
。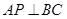 ;
;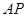 上是否存在点M,使得二面角
上是否存在点M,使得二面角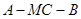 为直二面角?若存在,求
为直二面角?若存在,求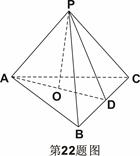
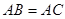 ,D是BC的中点,得
,D是BC的中点,得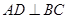 ,又
,又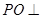 平面ABC,得
平面ABC,得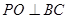 ,因为
,因为 ,所以
,所以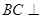 平面PAD,故
平面PAD,故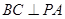 ‘利用线面垂直的性质定理得到。
‘利用线面垂直的性质定理得到。 于M,连接CM,由(1)中知
于M,连接CM,由(1)中知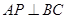 ,得
,得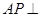 平面BMC,
平面BMC,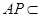 平面APC,所以平面
平面APC,所以平面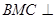 平面APC,在
平面APC,在 中,
中, ,得
,得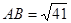 ,在
,在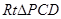 中,
中,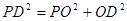 。
。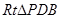 中,
中,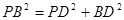 。
。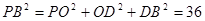 ,得
,得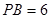
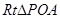 中,
中,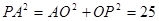 ,得
,得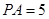
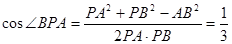 。
。
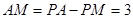 综上所述,存在点M符合题意AM=3
综上所述,存在点M符合题意AM=3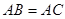 ,D是BC的中点,得
,D是BC的中点,得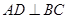 ,
,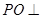 平面ABC,得
平面ABC,得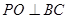 ,因为
,因为 ,
,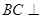 平面PAD,故
平面PAD,故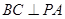 ………….4分
………….4分 于M,连接CM,由(1)中知
于M,连接CM,由(1)中知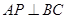 ,得
,得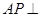 平面BMC,
平面BMC,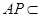 平面APC,所以平面
平面APC,所以平面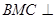 平面APC,……….6分,
平面APC,……….6分, 中,
中, ,得
,得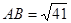 ,
,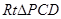 中,
中,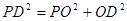 。
。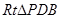 中,
中,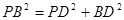 。
。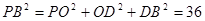 ,得
,得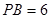
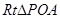 中,
中,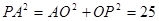 ,得
,得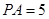
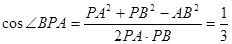 。
。 ………….10分
………….10分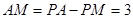


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源:不详 题型:解答题
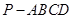 的底面是正方形,
的底面是正方形,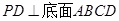 ,点E在棱PB上。
,点E在棱PB上。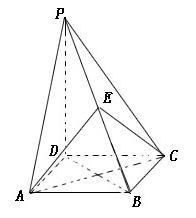
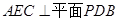 ;
;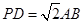 且E为PB的中点时,求AE与平
且E为PB的中点时,求AE与平查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
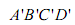 ,其中A与A '重合,且BB'<DD'<CC'.
,其中A与A '重合,且BB'<DD'<CC'.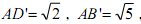 ,正方形的边长为
,正方形的边长为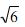 ,
, 的余弦值.
的余弦值.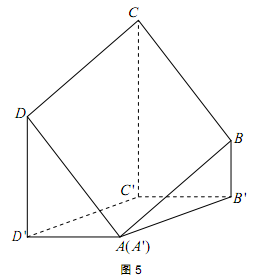
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中,
中, ="2" ,
="2" ,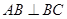 .点
.点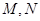 分别是
分别是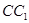 ,
,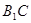 的中点,
的中点,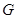 是棱
是棱 上的动点.
上的动点.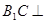 平面
平面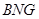 ;
;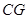 //平面
//平面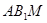 ,试确定
,试确定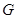 点的位置,
点的位置, 的余弦值.
的余弦值.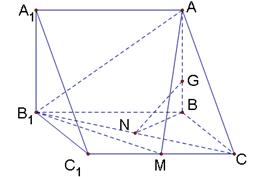 【
【查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
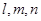 是三条不同的直线,
是三条不同的直线,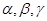 是三个不同的平面,现给出四个命题:
是三个不同的平面,现给出四个命题: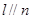 且
且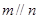 ,则
,则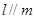 ; ②若
; ②若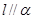 且
且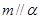 ,则
,则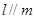 ;
;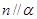 且
且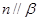 ,则
,则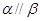 ; ④若
; ④若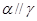 且
且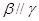 ,则
,则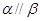 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
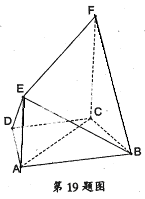
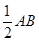 ,∠ACF=∠ADC=
,∠ACF=∠ADC=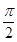 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com