
【题目】如图1,等腰![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的四等分点,且
的四等分点,且![]() .现沿
.现沿![]() ,
,![]() ,
,![]() 折叠成图2所示的几何体,使
折叠成图2所示的几何体,使![]() .
.
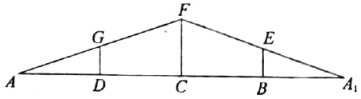
(图1)
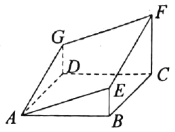
(图2)
(1)证明:![]() 平面
平面![]() ;
;
(2)求几何体![]() 的体积.
的体积.
科目:高中数学 来源: 题型:
【题目】设数列![]() 满足:①
满足:①![]() ;②所有项
;②所有项![]() ;③
;③ ![]() .
.
设集合![]() ,将集合
,将集合![]() 中的元素的最大值记为
中的元素的最大值记为![]() .换句话说,
.换句话说, ![]() 是
是
数列![]() 中满足不等式
中满足不等式![]() 的所有项的项数的最大值.我们称数列
的所有项的项数的最大值.我们称数列![]() 为数列
为数列![]() 的
的
伴随数列.例如,数列1,3,5的伴随数列为1,1,2,2,3.
(1)若数列![]() 的伴随数列为1,1,1,2,2,2,3,请写出数列
的伴随数列为1,1,1,2,2,2,3,请写出数列![]() ;
;
(2)设![]() ,求数列
,求数列![]() 的伴随数列
的伴随数列![]() 的前100之和;
的前100之和;
(3)若数列![]() 的前
的前![]() 项和
项和![]() (其中
(其中![]() 常数),试求数列
常数),试求数列![]() 的伴随数列
的伴随数列![]() 前
前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值和最小值;
的最大值和最小值;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校进入高中数学竞赛复赛的学生中,高一年级有8人,高二年级有16人,高三年级有32人,现釆用分层抽样的方法从这些学生中抽取7人进行釆访.
(1)求应从各年级分别抽取的人数;
(2)若从抽取的7人中再随机抽取2人做进一步了解(注高一学生记为![]() ,高二学生记为
,高二学生记为![]() ,高三学生记为
,高三学生记为![]() ,
,![]()
①列出所有可能的抽取结果;
②求抽取的2人均为高三年级学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中:
①已知点![]() ,动点
,动点![]() 满足
满足![]() ,则点
,则点![]() 的轨迹是一个圆;
的轨迹是一个圆;
②已知![]() ,则动点
,则动点![]() 的轨迹是双曲线;
的轨迹是双曲线;
③两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1;
④在平面直角坐标系内,到点![]() 和直线
和直线![]() 的距离相等的点的轨迹是抛物线;
的距离相等的点的轨迹是抛物线;
正确的命题是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P﹣ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB.
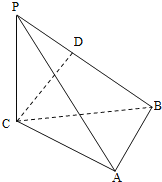
(1)求证:AB⊥平面PCB;
(2)求二面角C﹣PA﹣B的大小的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小组有7个同学,其中4个同学从来没有参加过天文研究性学习活动,3个同学曾经参加过天文研究性学习活动.
(1)现从该小组中随机选2个同学参加天文研究性学习活动,求恰好选到1个曾经参加过天文研究性学习活动的同学的概率;
(2)若从该小组随机选2个同学参加天文研究性学习活动,则活动结束后,该小组有参加过天文研究性学习活动的同学个数![]() 是一个随机变量,求随机变量
是一个随机变量,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com